-
[Machine Learning] PCA(Principal Component Analysis)Informatik 2022. 2. 9. 06:12반응형
PCA는 고차원의 데이터를 저차원의 데이터로 환원시키는 기법을 말한다. [wikipedia]
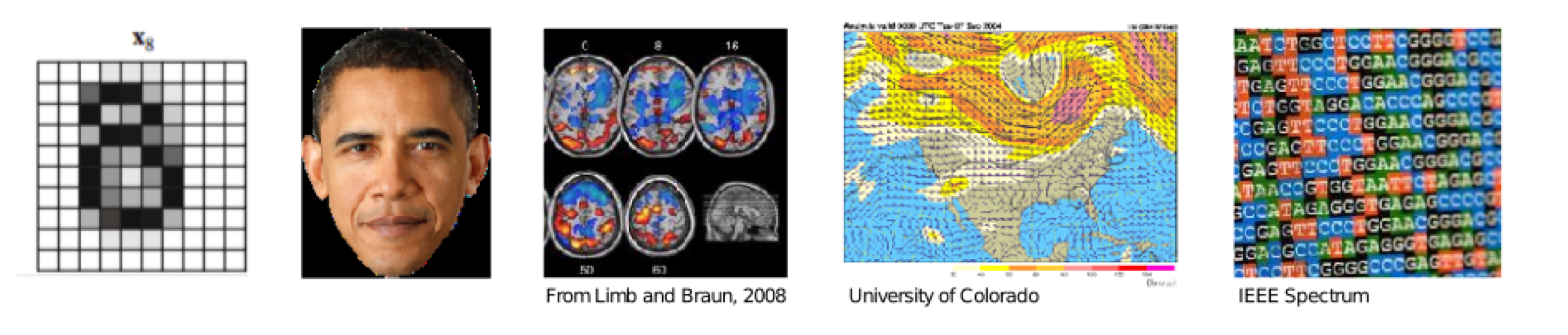
머신러닝에 있어서 대부분의 데이터는 매우 고차원이며 데이터 양은 광대하다. 그렇기에 초고차원 데이터에 표준 회귀(Regression)나 분류(Classification) 기법을 적용하기에는 부적절하다.
베이즈 결정 이론에서의 MLE (데이터가 평균값이 다르고, 공분산이 같은 다변량 정규분포를 따를 때):
$$arg \max_i P(w_i | \mathbf {x}) = arg\max_i \left [\mathbf {x}^{\top} \Sigma^{-1} \mu_i - \frac {1}{2} \mu_i^{\top} \Sigma^{-1} \mu_i + \log P(w_i) \right ]$$
이전에 배웠던 베이즈 결정 이론을 살펴보면 베이즈 분류를 하기 위해서는 데이터의 공분산인 $\Sigma$를 구해야 했었다. 실생활에서 학습 데이터만으로는 실제 공분산 $\Sigma$을 알 수 없기에 공분산의 추정 값인 $\hat {\Sigma}$를 대신 사용한다. 하지만 주어지는 초고차원 학습 데이터로 어떻게 공분산의 추정 값의 역행렬 $\hat {\Sigma}^{-1}$을 정확하게 구할 수 있을까?MLE로 계산한 다변량 정규분포의 공분산 추정값:
$$\begin {gather} \begin {aligned} \hat {\Sigma} &= \frac {1}{N} \sum^N_{k = 1} (x_k - \mu)(x_k - \mu)^{\top} \\ &= \frac {1}{N} \overline {X} \ \overline {X}^{\top} \end {aligned} \\ \text {where } \overline {X} \text { is a matrix of size } d \times N \text { containing the centered data} \end {gather}$$실제 공분산을 대신해 계산하려던 공분산의 추정 값의 역행렬 $\hat {\Sigma}^{-1}$을 구하는 데에도 몇 가지 한계점이 있다. 우선, 공분산의 추정 값의 역행렬이 존재하기 위해서는 $d \leq N$일 때, $rank(\overline {X}) = d$를 만족해야 한다. 또한, 공분산은 데이터의 의존성을 나타내는 수치이므로 데이터가 변할 때마다 공분산도 같이 따라 변하기 때문에 비정상성(Non-stationary) 특징을 띤다. 따라서 매우 고차원 데이터로 알맞은 공분산의 추정 값을 주기적으로 구하는 것은 계산적으로 손실이 매우 크다. 그렇기에 PCA으로 적용해 데이터의 차원을 줄여, 데이터의 고차원 문제를 해결한다.
※ If $A$ is $m$-by-$n$ and the rank of $A$ is equal to $n (n \leq m)$, then $A$ has a left inverse, an $n$-by-$m$ matrix $B$ such that $BA = I_n$. If $A$ has rank $m (m \leq n)$, then it has a right inverse, an $n$-by-$m$ matrix $B$ such that $AB = I_m$ [wikipedia]
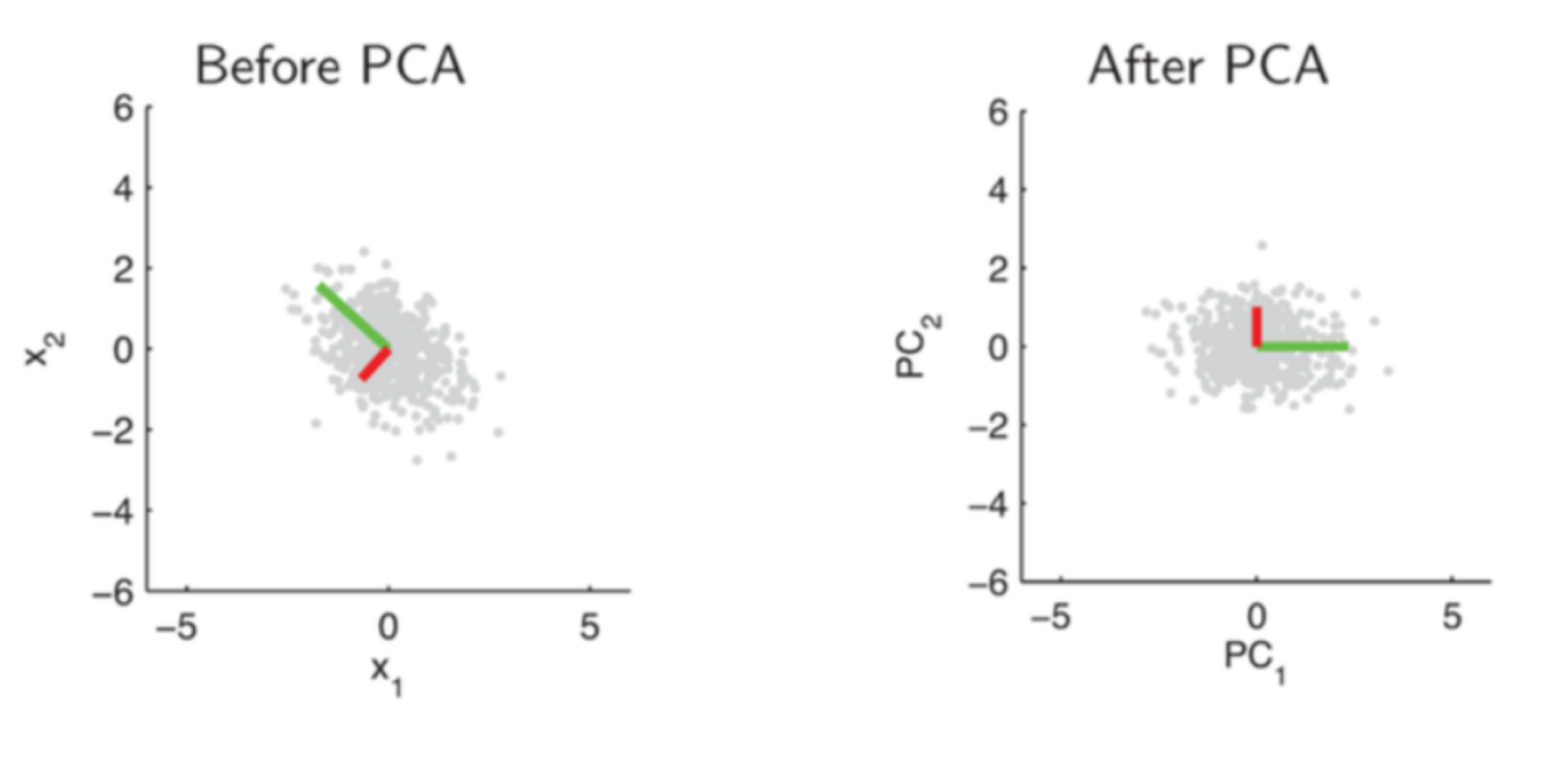
PCA가 고차원의 데이터를 저 차원으로 환원시킨다고 했는데, 자세히 말하자면 고차원 데이터를 저차원으로 선형적으로 매핑(Mapping)하여 차원을 축소하는 회귀(Regression) 기법이다. 아래 그림은 2차원 데이터의 PCA 기법 적용의 예이다. 데이터의 특성을 가장 잘 살려 선형적 매핑하기 위해 노이즈(Noise)는 최소화하는 반면 신호(Signal)는 최대화하는 선 $w$를 찾는 것이 목표이다.
※ PCA는 저차원 가우시안 분포(Gaussian Distribution)를 따르는 데이터에만 최적의 결과를 낳는다.

노이즈 최소화(Noise Minimization)
데이터 세트 $x_1,..., x_N \in \mathbb {R}^d$가 최소 거리(Minimum Distance)로 매핑될 수 있는 일차원 부분 공간(Subspace)을 찾아라.

- 모델(Model): 일차원 부분 공간에 정사영되는 데이터 세트들을 말한다. $$\hat {\mathbf {x}} = \mathbf {w} \mathbf {w}^{\top} \mathbf {x}, \text { with } ||\mathbf {w}|| = 1$$
- 노이즈 최소화: 실제 데이터 세트와 정사영된 데이터 세트들의 거리가 가장 일차원 부분 공간을 구한다. $$arg \min_w \bigg [ \frac {1}{N} \sum^{N}_{k = 1} || \mathbf {x} - \underbrace {\mathbf {w} \mathbf {w}^{\top} \mathbf {x}}_{\hat {\mathbf {x}}} ||^2 \bigg ]$$
신호 최대화(Signal Maximization)
데이터 세트 $x_1,..., x_N \in \mathbb {R}^d$가 최대 분산(Maximum Variance)을 갖게끔 매핑될 수 있는 일차원 부분 공간을 찾아라.

- 모델: $$h = \mathbf {w}^{\top} \mathbf {x}, \text { with } ||\mathbf {w}|| = 1$$
- 신호 최대화: 정사영된 데이터 세트들의 분산을 최대화하는 일차원 부분 공간을 구한다. $$arg \max_w \bigg [ \frac {1}{N} \sum^{N}_{k = 1} (\mathbf {w}^{\top} \mathbf {x}_k - \mathbb {E} [\underbrace {\mathbf {w}^{\top} \mathbf {x}}_{h}])^2 \bigg ]$$ 데이터를 가운데로 정렬하면 $\mathbb {E} [\mathbf {x}] = 0$이므로 다음과 같이 다시 쓰일 수 있다. $$arg \max_w \bigg [ \frac {1}{N} \sum^{N}_{k = 1} (\mathbf {w}^{\top} \mathbf {x}_k)^2 \bigg ]$$
노이즈 최소화에서 신호 최대화로의 유도(From Min Noise to Max Signal)
데이터를 가운데로 정렬했을 때, 노이즈 최소화에서 신호 최대화가 같음을 다음과 같이 증명할 수 있다.

노이즈 최소화나 신호 최대화는 모든 데이터를 고려해 평균값을 내기 때문에 이상치(Outlier)를 따로 고려하지 않는다.
라그랑주 승수법(Lagrange Multipliers)
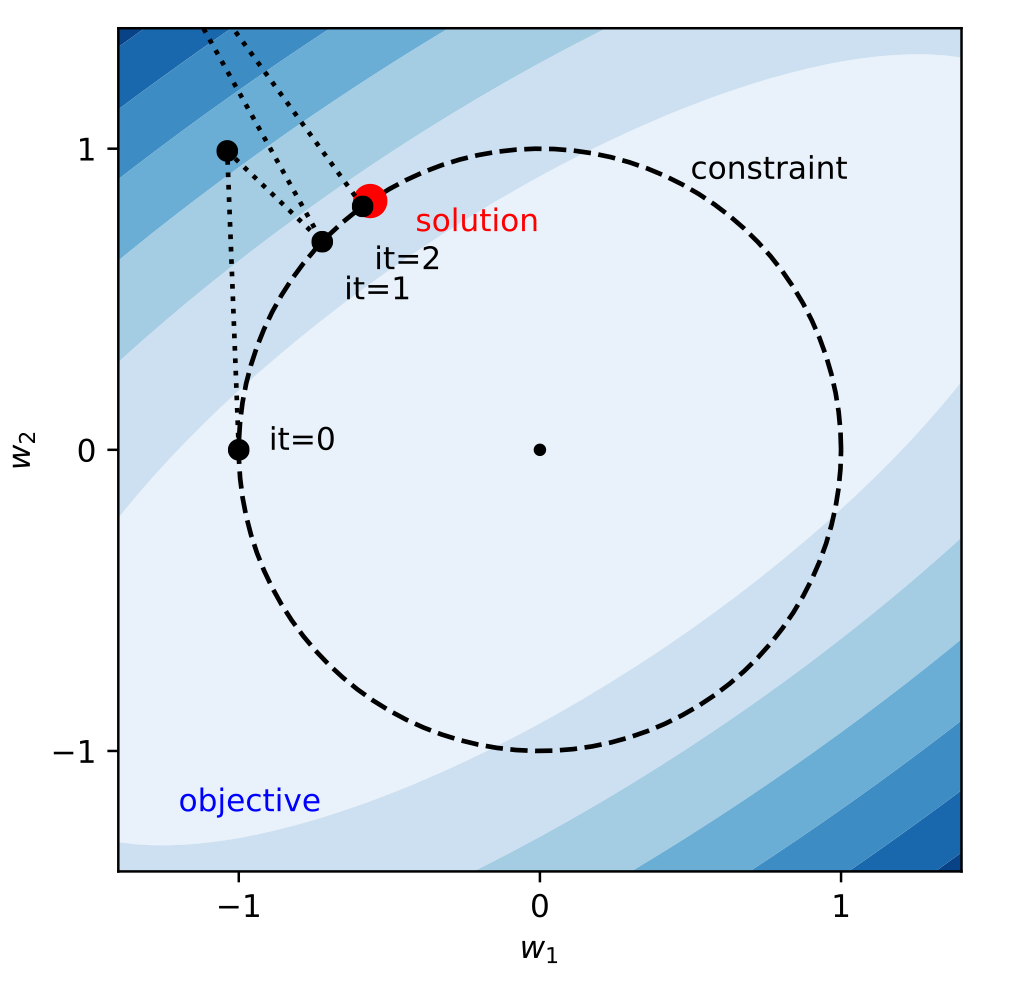
노이즈 최소화와 신호 최대화에서 설립했던 모델로 알맞은 $\mathbf {w}$를 찾는 것을 목표로 삼았고 이제는 어떻게 모델 $\mathbf {w}$을 효과적으로 찾을 것인가를 알아본다. 아래의 그림은 제약이 있는 어떤 문제에서 라그랑주 승수법으로 두 개의 모수(Parameter)의 최적점을 찾는 것을 보여준다.

라그랑주 승수법의 예 
$g(\theta) = 0$인 제약 아래 $arg \max_{\theta} f(\theta)$를 최적화하는 문제를 생각하자.
- 라그랑지언(Lagrangian)을 설립한다. $$\mathcal {L}(\theta, \lambda) = f(\theta) + \lambda g(\theta)$$ where $\lambda$ is called the Lagrange multiplier.
- 아래의 식을 푼다. $$\nabla \mathcal {L}(\theta, \lambda) = 0$$ which is a necessary condition for the condition.
예 1) 이차원 함수에 대한 라그랑주 승수법

예 2)
$\mathbf {x}_1, ..., \mathbf {x}_N \in \mathbb {R}^d$를 $N$개의 데이터를 가지고 있는 데이터 세트라고 할 때, 다음과 같이 모수 $\mathbf {\theta} \in \mathbb {R}^d$에 대해서 최소화하려는 목적 함수(Objective Function)을 고려하자.
$$J(\mathbf {\theta}) = \sum^{N}_{k = 1} || \mathbf {\theta} - \mathbf {x}_k ||^2$$

아무런 제약 조건 없이는 위의 목적 함수를 최소화시키는 $\mathbf {\theta}$는 경험적으로 근거한 평균 $\mathbf {m} = \frac {1}{N} \sum^{N}_{k = 1} \mathbf {x}_k$이다. 그러나, 일반적으로 모수에 대한 제약 조건이 주어지기 때문에 라그랑주 승수법을 이용해 풀이해야 한다.
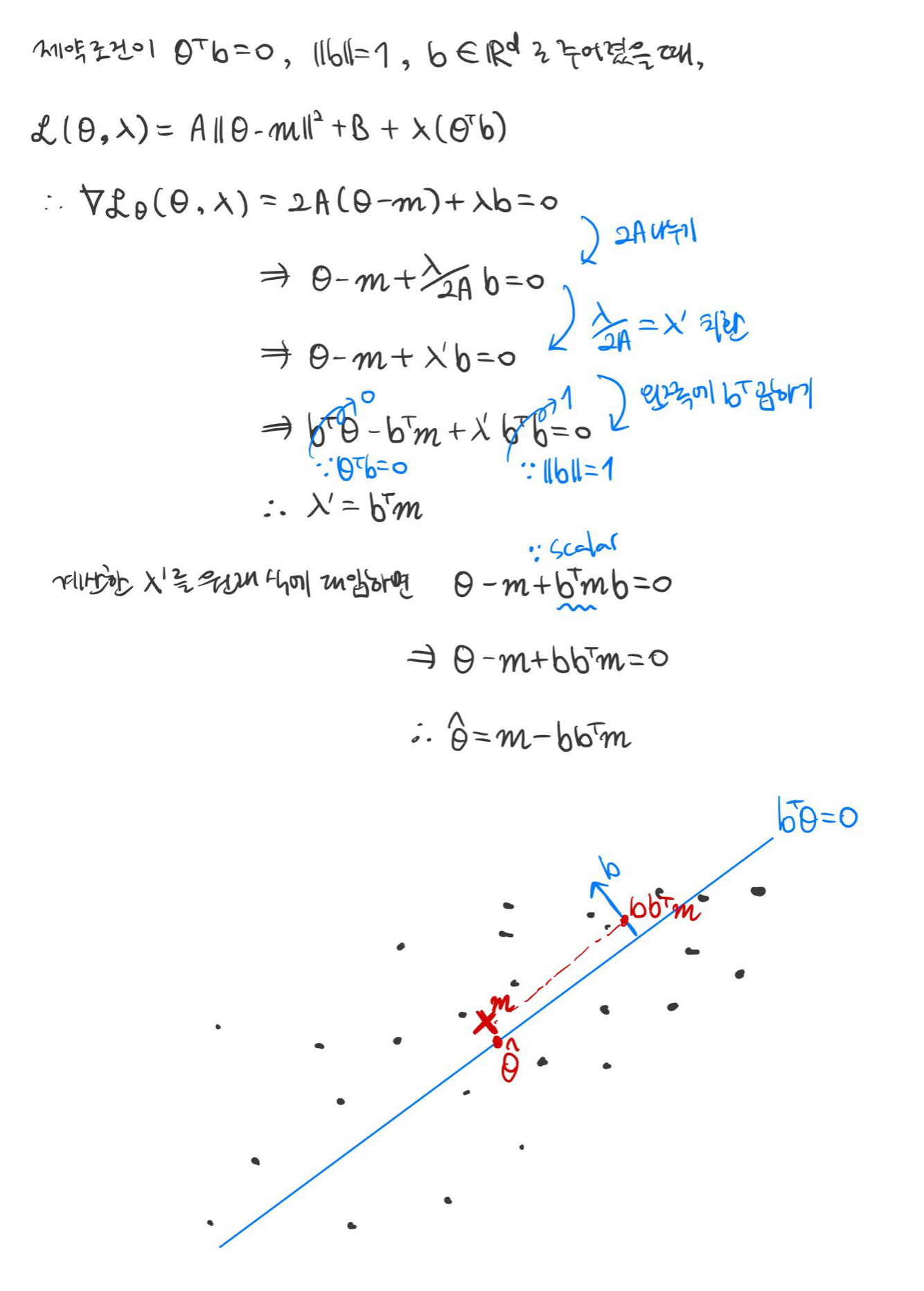

라그랑주 승수법을 이용한 PCA 솔루션 구하기
신호 최대화(Signal Maximization)
$$arg \max_{\mathbf {x}} \left [ \frac {1}{N} \sum^{N}_{k = 1} (\mathbf {x}^{\top}_k \mathbf {w})^2 \right ] \ \ \ \text {s.t.} || \mathbf {w} || = 1$$
공분산의 추정 값 $\hat {\Sigma}$은 $\mathbf {w}$에 독립적이며 미리 계산해놓을 수 있다.

PCA 문제를 풀기 위해서는 공분산 추정 값 $\hat {\Sigma}$이 필요하고, 라그랑주 승수법을 이용하면 결론적으로 최적의 $\mathbf {w}$를 구하는 것이 공분산 추정 값 $\hat {\Sigma}$의 고유 벡터(Eigenvector)를 구하는 것과 같음을 알 수 있다. 가장 큰 고유 값을 주요 성분 $\mathbf {w}$이라 하며, 이에 데이터를 정사영 시키면 데이터의 특성을 가장 잘 살리는 방향으로 데이터들을 확대/축소, 회전해 차원을 축소할 수 있다.
※ PCA를 적용하면 데이터는 자동으로 0으로 정렬된다.
예 1)
데이터 세트 $\mathbf {x}_1, ..., \mathbf {x}_N \in \mathbb {R}^d$가 주어졌을 때, PCA는 데이터의 분산을 최대화하는 방향으로 데이터를 정사영시킬 수 있는 단위 벡터 $\mathbf {u} \in \mathbb {R}^d$를 찾고자 한다. 다음 문제를 최적화하면 해당 단위 벡터를 얻을 수 있다.
$$arg \max_{\mathbf {u}} \frac {1}{N} \sum^{N}_{k = 1} \left [ \mathbf {u}^{\top} \mathbf {x}_k - \frac {1}{N} \left (\sum^{N}_{l = 1} \mathbf {u}^{\top} \mathbf {x}_l \right ) \right ]^2 \ \ \ \text {with } ||\mathbf {u}||^2 = 1$$
ㅇ

예 2) 고윳값의 경계(Bounds on Eigenvalues)
$\lambda_1$가 산점도 행렬(Scatter Matrix) $\mathbf {S}$의 가장 큰 고윳값이라고 하자. 고윳값 $\lambda_1$는 데이터를 제 1 주성분으로 정사영했을 때, 데이터의 분산을 나타낸다. 하지만 고윳값을 계산하는 것은 계산적으로 비싸기 때문에 $\mathbf {S}$의 대각 성분(Diagonal Element)을 이용해 어떻게 경계값을 찾을 수 있는지 증명하자.

SVD(Singular Value Decomposition)
SVD는 행렬을 특정한 구조로 분해하는 방식으로, 스펙트럼 이론()을 이용하여 직교 정사각 행렬을 고윳값을 기저로 하여 대각 행렬(Diagonal Matrix)로 분해한다. [wikipedia]
행렬 $M$은 다음과 같은 세 행렬의 곱으로 분해할 수 있다.
- $U$ $m \times m$ 크기를 가지는 유니터리 행렬(Unitary Matrix)으로 $MM^{\top}$의 고유 벡터를 포함한다.
- $V$는 $n \times n$ 크기를 가지는 유니터리 행렬로 $M^{\top} M$의 고유 벡터를 포함한다.
- $\Lambda$는 $m \times n$ 크기를 가지며 $MM^{\top}$의 고윳값의 제곱으로 구성된 대각 행렬이다.
SVD를 이용한 PCA 솔루션 구하기
$M = \frac {1}{\sqrt {N}} \overline {X}$으로 설정 시 SVD로 행렬 $M$을 분해할 수 있다.
- 공분산 추정 값 $\hat {\Sigma}$의 고유 벡터, 즉, 주성분을 포함하는 $U = (\mathbf {w}_1 |... | \mathbf {w}_d)$
- $\Lambda = diag(\sqrt {\lambda_1},..., \sqrt {\lambda_d})$ (※ 고윳값에 제곱을 취해도 고윳값 크기 순은 바뀌지 않는다.)
라그랑주 승수법과 SVD 비교
라그랑스 승수법을 이용한 방법보다 SVD로 PCA를 훨씬 더 빠르게 계산할 수 있고, 공분산 추정 값을 구하지 않아도 돼 더 안정적이다. SVD의 계산 복잡도(Computational Complexity)가 $\mathcal {O} (\min (N^2 d, d^2 N))$인 반면 라그랑주 승수법은 $\mathcal {O} (d^3)$를 갖는다. 그렇지만, SVD에서 $d \approx N인 경우, 공분산 추정 값의 고유 벡터를 구하는 라그랑주 승수법의 계산 복잡도와 같아진다. 이는 다른 말로 데이터 차원이 매우 클 경우 SVD로 계산적 이득을 얻을 수 없음을 의미한다. PCA 실사용에서는 최상 몇 개의 주성분을 구하는데, SVD는 모든 주성분을 구하기 때문에 사용하지 않는 나머지 성분들은 불필요하게 계산된다라고 할 수 있겠다.
멱방법(Power Iteration)
멱방법은 주요 성분을 좀 더 빨리 계산할 수 없을까에 대한 해답을 제시한다. 임의의 단위 벡터(Unit Vector) $\mathbf {w}^{(0)}$부터 시작해 다음과 같은 방법을 $T$번 반복하여 첫번째 주성분을 찾을 수 있다. 멱방법은 기하급수적으로 매우 빠르게 항상 수렴한다. 또한, 최상의 고유 벡터만을 구하기 때문에 더 효율적으로 할 수 있다.
$$\mathbf {v}^{(t)} \leftarrow \hat {\Sigma} \mathbf {w}^{(t - 1)}$$
$$\mathbf {w}^{(t)} \leftarrow \frac {\mathbf {v}^{(t)}}{|| \mathbf {v}^{(t)} ||}$$
예 1)

PCA 기법의 응용(Applications of PCA)

PCA 응용: 데이터 압축 1 
PCA 응용: 데이터 압축 2
1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.
2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.
반응형'Informatik' 카테고리의 다른 글
[Machine Learning] 경사 하강법(Gradient Descent) (0) 2022.02.09 [Machine Learning] 최대우도법(Maximum Likelihood Estimation) (0) 2022.02.09 [Machine Learning] 최대우도법 vs. 베이즈 추정법(Maximum Likelihood Estimation vs. Bayesian Estimation) (0) 2022.01.31 [Machine Learning] 단순 선형 회귀(Simple Linear Regression) (0) 2022.01.28 [Machine Learning] 회귀(Regression) (0) 2022.01.23