-
[Machine Learning] 최대우도법(Maximum Likelihood Estimation)Informatik 2022. 2. 9. 21:13반응형
최대우도법은 어떤 확률 변수(Random Variable)에서 표집한 값들을 토대로 그 확률 변수의 모수(Parameter)를 구하는 방법이다. 어떤 모수가 주어졌을 때, 원하는 값들이 나올 우도(Likelihood)를 최대로 만드는 모수를 선택한다. [wikipedia]
평균(Mean)이나 공분산(Covariance)으로 이루어진 모수 벡터(Parameter Vector) $\theta$와 데이터에 대한 확률 밀도 함수(Probability Density Function) $p(\mathbf {x} | \theta)$를 가정할 때, 데이터를 가장 잘 모델링할 수 있는, 즉, 최대 우도를 갖는 모수 $\theta$들을 찾고자 한다.
- 데이터 세트(Dataset) $\mathcal {D} = (\mathbf {x}_1,..., \mathbf {x}_N)$
- 데이터의 각 예시 $\mathbf {x}_k \in \mathbb {R}^d$는 독립적으로 같은 밀도 함수 $p(\mathbf {x} | \theta)$에 의해 생성한다.
- 결합 확률 밀도 함수(Joint Density Function)는 다음과 같다. $$p(\mathcal {D} | \theta) = \prod^{N}_{k = 1} p(\mathbf {x}_k | \theta)$$. 이를 데이터 세트 $\mathcal {D}$에 대하여 $\theta$의 우도라고 한다.
- $\mathcal {D}$에 대하여 $\mathbf {\theta}$의 우도가 가장 큰 $\theta$를 선택한다. $\hat {\theta} = arg \max_{\theta} p(\mathcal {D} | \theta)$
※ 편리성을 위해, $p(\mathcal {D} | \theta) = \prod^{N}_{k = 1} p(\mathbf {x}_k | \theta)$ 대신 로그 우도(Log-Likelihood) $\log p(\mathcal {D} | \theta) = \sum^{N}_{k = 1} \log p(\mathbf {x}_k | \theta)$를 구한다.Q. 우도 대신 로그 우도를 대신 구하는 이유는?
A. $p(\mathbf {x}_k | \theta)$는 모수에 대한 데이터의 가능성을 나타내기 때문에 작은 값을 가질 확률이 높다. $p(\mathcal {D} | \theta)$를 구하기 위해 $p(\mathbf {x}_k | \theta)$를 모두 곱하면, 매우 작은 값을 갖게 되어 컴퓨터에서의 계산이 어려울 수가 있다. 따라서 단조 증가함수(Monotonically Increasing Function)인 로그 함수(Log Function)를 적용하여 결괏값에 영향을 끼치지 않고 수월하게 MLE을 구할 수 있다.
따라서 최적의 모수를 찾는 MLE는 다음의 식과 같다.$$\hat {\theta} = arg \max_{\theta} \log p(\mathcal {D} | \theta) = arg \max_{\theta} \sum^{N}_{k = 1} \log p(\mathbf {x}_k | \theta)$$
예시 1) 오류가 가우시안 분포(Gaussian Distribution)를 따를 때($y = f(\mathbf {x}) + \epsilon, \epsilon \sim \mathcal {N} (0, \sigma^2)$)
위의 모델 $y$에 대한 사후 확률(Posterior Probability)은 $p(y | \mathbf {x}, f, \sigma^2)$으로 $\mathcal {N} (y | f(\mathbf {x}), \sigma^2)$ 분포를 갖는다.
학습 예시 $(\mathbf{x}_1, y_1), (\mathbf {x}_2, y_2),..., (\mathbf {x}_m, y_m) \in \mathbb {R}^m \times \mathbb {R}$가 $P(\mathbf {x}, y) = p(y | \mathbf {x}) P(\mathbf {x})$로부터 독립적으로 생성된다고 가정하자.

위의 그림에서 MLE로 최적의 가설을 찾는 것은 MSE를 최소화하는 것과 같음을 증명한다.
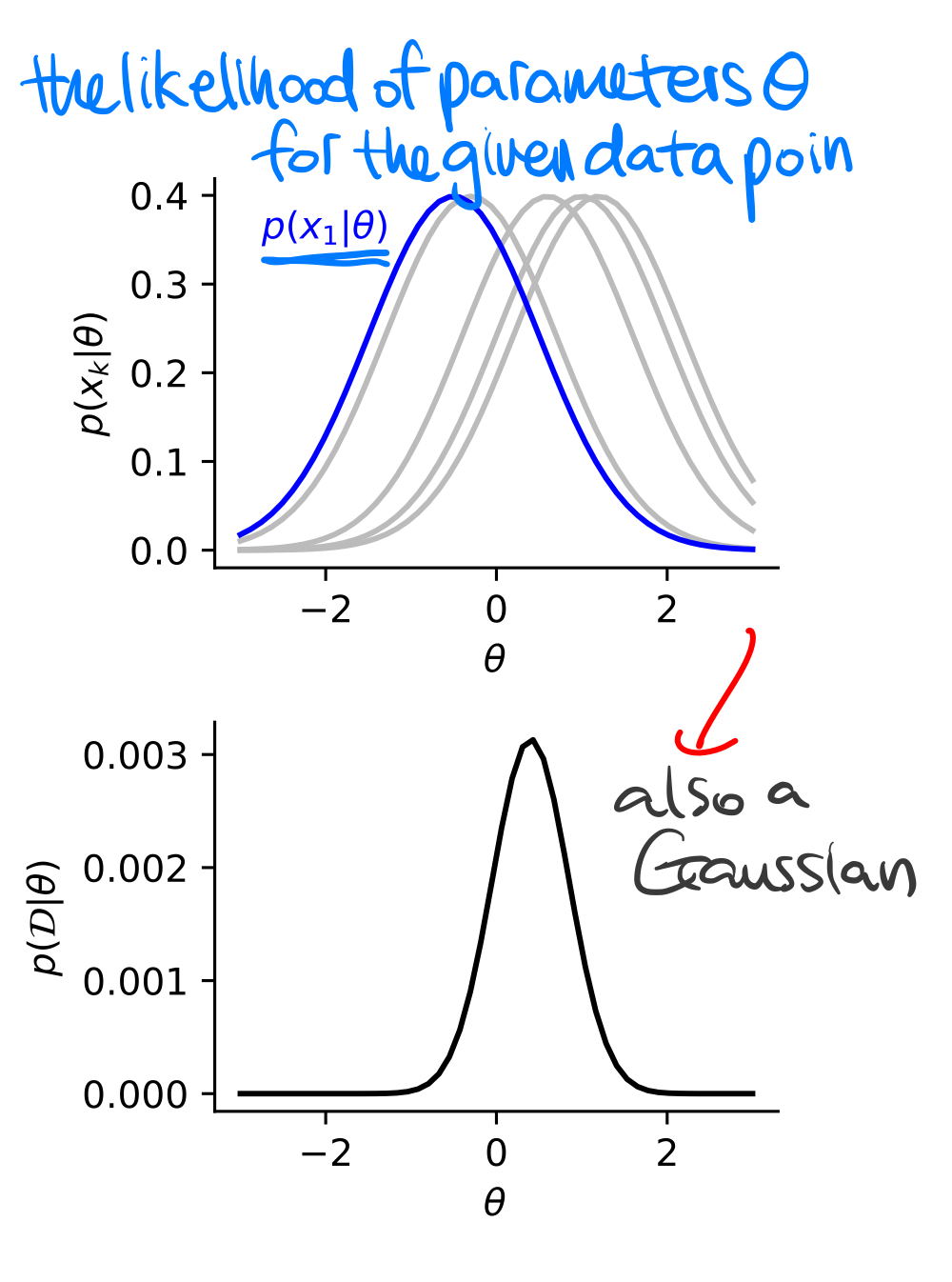
예시 2) 정규 분포($\mathbf {x} \sim \mathcal {N} (\theta, 1)$)
해당 모델의 데이터 $\mathbf {x}_k$의 밀도 함수는 다음과 같이 쓸 수 있다.
$$p(\mathbf {x}_k | \theta) = \frac {1}{\sqrt {2 \pi}} \exp (- \frac {1}{2}(x_k - \theta)^2)$$
모든 데이터들이 독립적으로 생성되었다는 가정하에 결합 우도와 로그 우도는 다음과 같다.
$$\begin {aligned} p(\mathcal {D} | \theta) &= \prod^N_{k = 1} \frac {1}{\sqrt {2 \pi}} \exp (- \frac {1}{2} (x_k - \theta)^2) \\ \log p(\mathcal {D} | \theta) &= \sum^N_{k = 1} \left [ -\frac {1}{2} \log 2 \pi - \frac {1}{2} (x_k - \theta)^2 \right ] \end {aligned}$$

예시 3) 다변량 정규분포(Multivariate Normal Distribution) ($\mathbf {x} \sim \mathcal {N} (\mu, \Sigma)$)
다변량 정규분포의 확률 밀도 함수(Multivariate Normal Distribution pdf):
$$p(\mathbf {x} | w_i) = \frac {1}{\sqrt{(2 \pi)^d \det(\Sigma_i)}} \exp {\left (-\frac {1}{2} (\mathbf {x} - \mu_i)^{\top} \Sigma^{-1}_i (\mathbf {x} - \mu_i) \right )}$$
다변량 정규분포의 평균값 추정 
다변량 정규분포의 공분산 추정
예시 4) 베루누이 분포(Bernoulli Distribution)
데이터 $x_1, ..., x_m$이 성공률(Success Probability) $p$를 갖는 베르누이 분포를 따를 때, MLE로 $\hat {p}$를 구하여라.
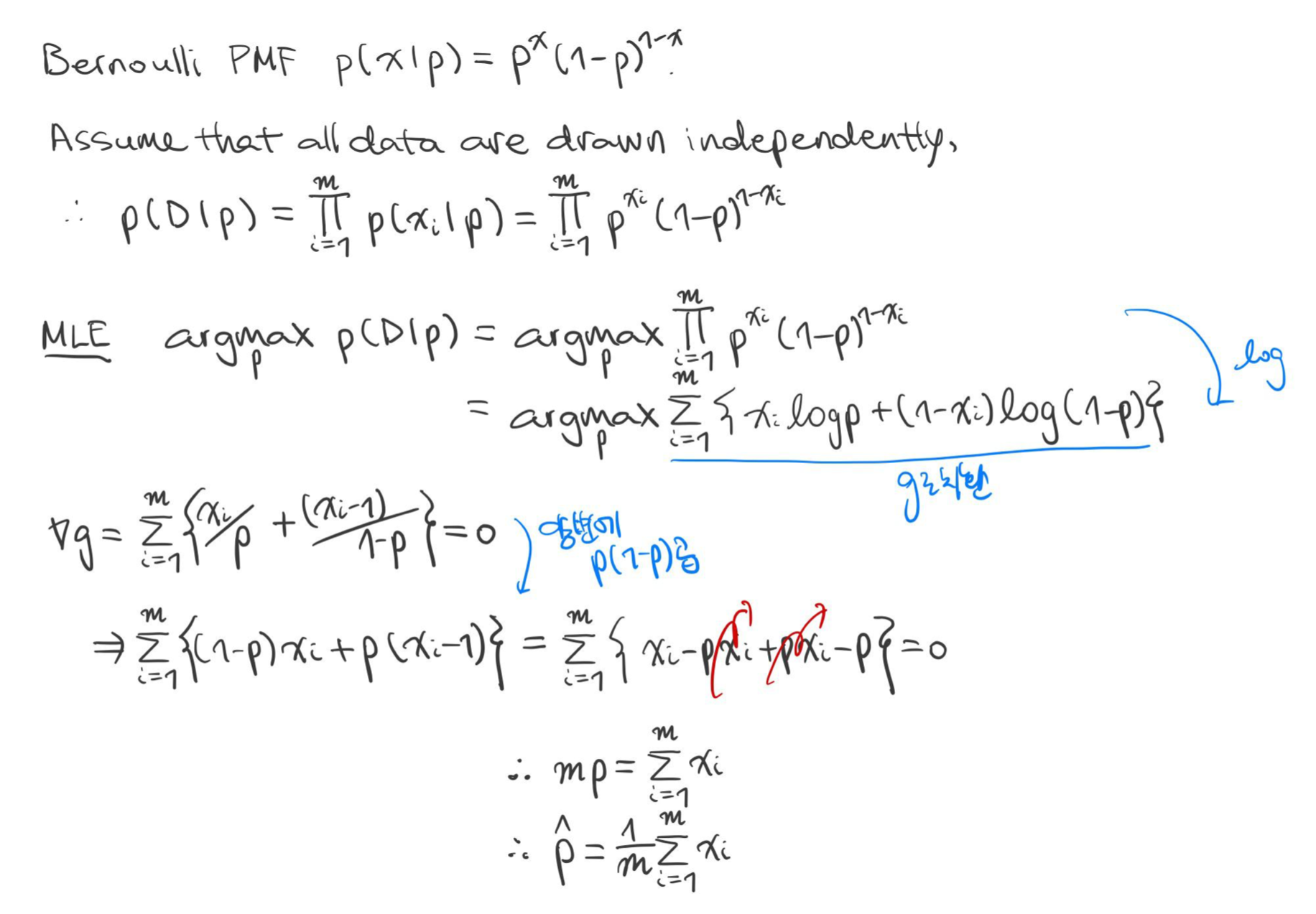
예시 5) $p(x, y) = \lambda \eta \exp^{- \lambda x - \eta y}, (\lambda, \eta > 0)$
위의 확률 분포를 따르는 데이터 세트 $\mathcal {D} = \{ (x_1, y_1),..., (x_N, y_N) \}$가 있다고 가정하자.
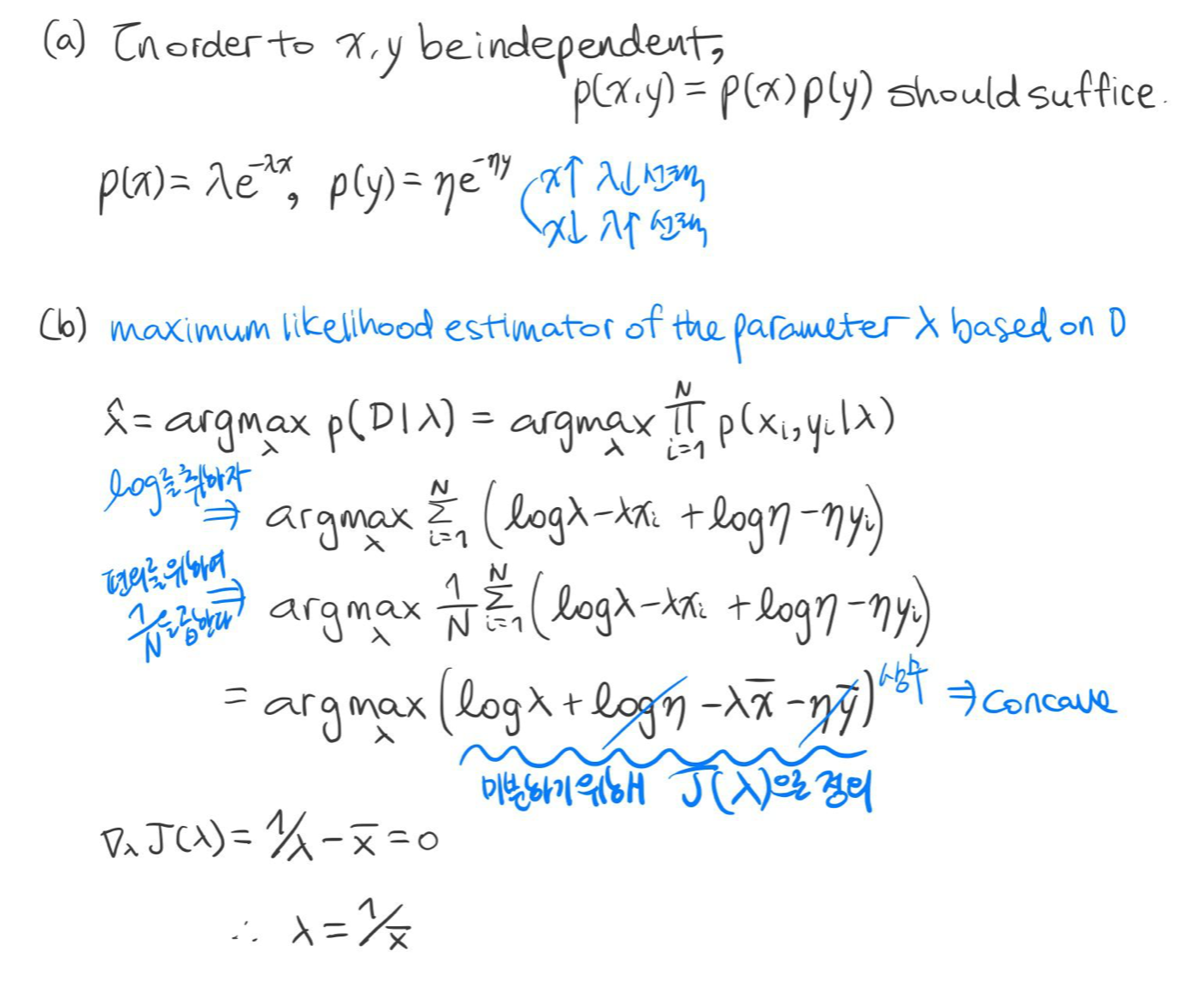

예 6) 기하 분포(Geometric Distribution)
아래의 그림은 기하 분포를 따르는 데이터를 두 클래스 $w_1$와 $w_2$로 분류하고자 하는 예를 보여준다. 각각 클래스를 50 % 확률로 분류할 수 있으며 알려지지 않은 모수 $\theta$와 그에 대한 확률 분포 $P(x = k | \theta) = (1 - \theta)^k \theta$로 데이터 세트 $\mathcal {D}_1$와 $\mathcal {D}_2$로 분류된다.
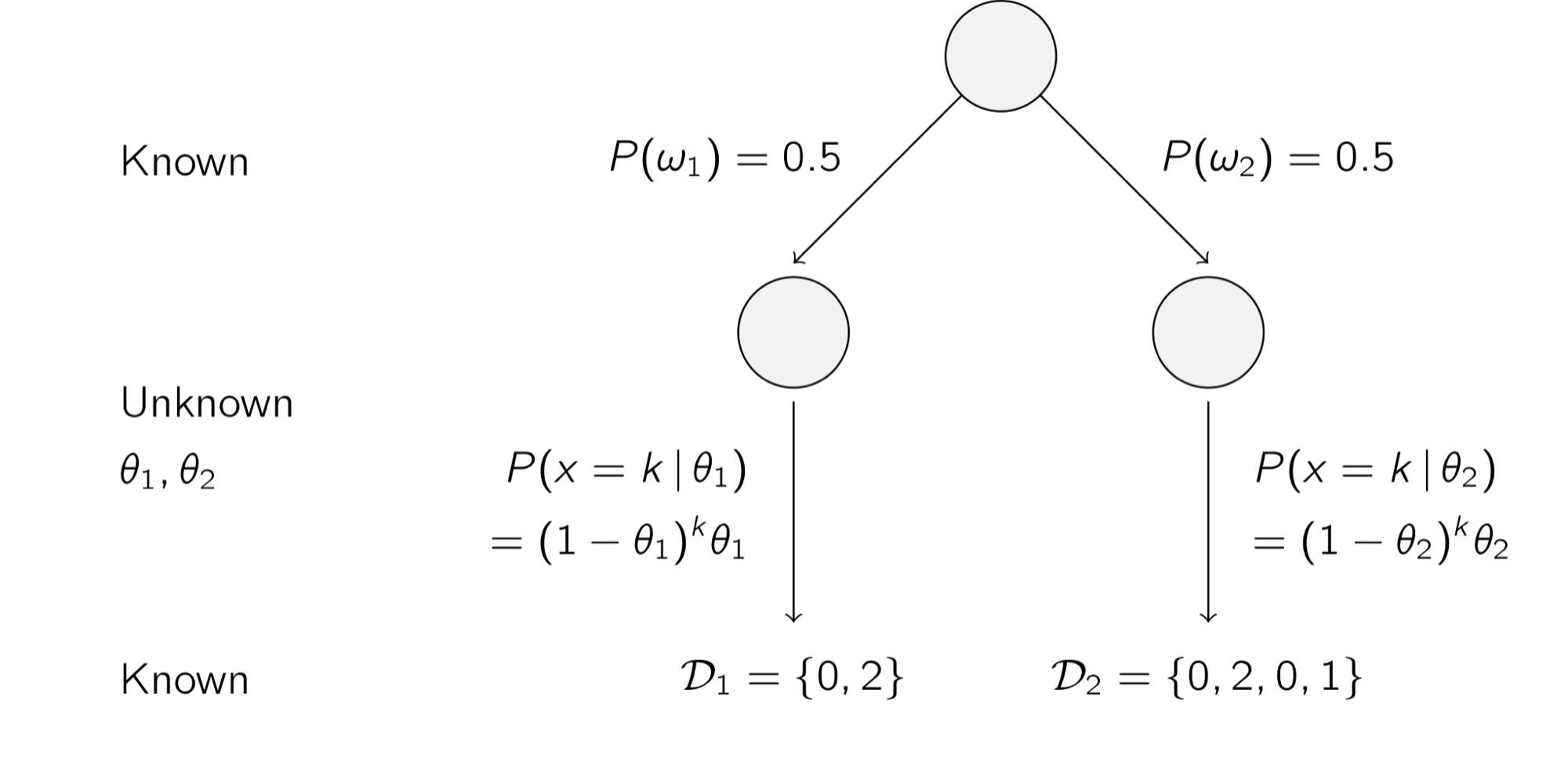

k = 1일 때의 분류기 예시 이처럼 MLE를 이용해 알려지지 않은 확률 분포 모수를 예측할 수 있으며, 예측한 모수에 베이즈 이론을 적용해 데이터를 분류한다.
반응형'Informatik' 카테고리의 다른 글
[Machine Learning] 다중 선형 회귀(Multiple Linear Regression) (0) 2022.02.12 [Machine Learning] 경사 하강법(Gradient Descent) (0) 2022.02.09 [Machine Learning] PCA(Principal Component Analysis) (0) 2022.02.09 [Machine Learning] 최대우도법 vs. 베이즈 추정법(Maximum Likelihood Estimation vs. Bayesian Estimation) (0) 2022.01.31 [Machine Learning] 단순 선형 회귀(Simple Linear Regression) (0) 2022.01.28