[Machine Learning] 모델 평가와 선택(Model Assessment and Selection)

※ 모델 선택에 있어서 중요한 개념: [Machine Learning] 오버 피팅(Overfitting)

[Machine Learning] 오버 피팅(Overfitting)

---

오차의 종류들(Types of Errors)

모델 평가(Model Assessment)란 주어진 가설(Hypothesis) $h \in$ F에 대해서 모델의 성능을 평가하는 것이다. 성능을 측정하는 데에는 크게 세 가지 요소가 있다.

• 학습 오차(Training Error): 학습 세트 $D_{train} = (x_1, y_1), (x_2, y_2), \cdots, (x_m, y_m)$에 대한 가설 $h$의 경험적 위험도(Empirical Risk) $E_m [h]$을 말한다. 
• 일반화 오차(Generalization Error): 입력 공간(Input Space) $\mathbb {R}^n \times \mathbb {R}$ 상의 확률 분포 $P(x, y)$를 가정할 때 기대 위험도(Expected Risk) $E [h]$를 지칭한다. 아직 관찰되지 않은 데이터에 대한 가설 $h$에 대한 기대되는 오차로 학습 오차보다 더 중요한 개념이다. 하지만, 확률 분포 $P(x, y)$는 미지수므로 일반화 오차로 모델 평가가 불가능하다. 
• 검정 오차(Test Error): 모델을 훈련시키는 데 사용하지 않는 데이터 세트, 즉, 검정 세트 $D_{test} = (x_1, y_1), (x_2, y_2), \cdots, (x_p, y_p)$에 대한 가설 $h$의 경험적 위험도 $E_p [h]$를 뜻한다. 검정 오차로 일반화 오차를 대신 추정할 수 있다.

---

모델 선택의 기준점

오캄의 면도날(Occam's Razor) 법칙:
"Entities must not be multiplied beyond necessity." [William of Ockham (1287-1347)]

반증 가능성(Falsifiability) 이론:
"A good model must accurately describe a large class of observations on the basis of a model that contains only a few arbitrary elements, and it must take definite predictions about the results of future observations." [S. Hawking, after K. Popper]

칼 포퍼의 반증 가능성 이론은 일반화 오차가 가장 작은 모델을 선호해야 함을 예시한다. 아래의 그림처럼 학습 오차가 0으로 수렴하더라도, 항상 일반화 오차가 감소하지 않는다. 

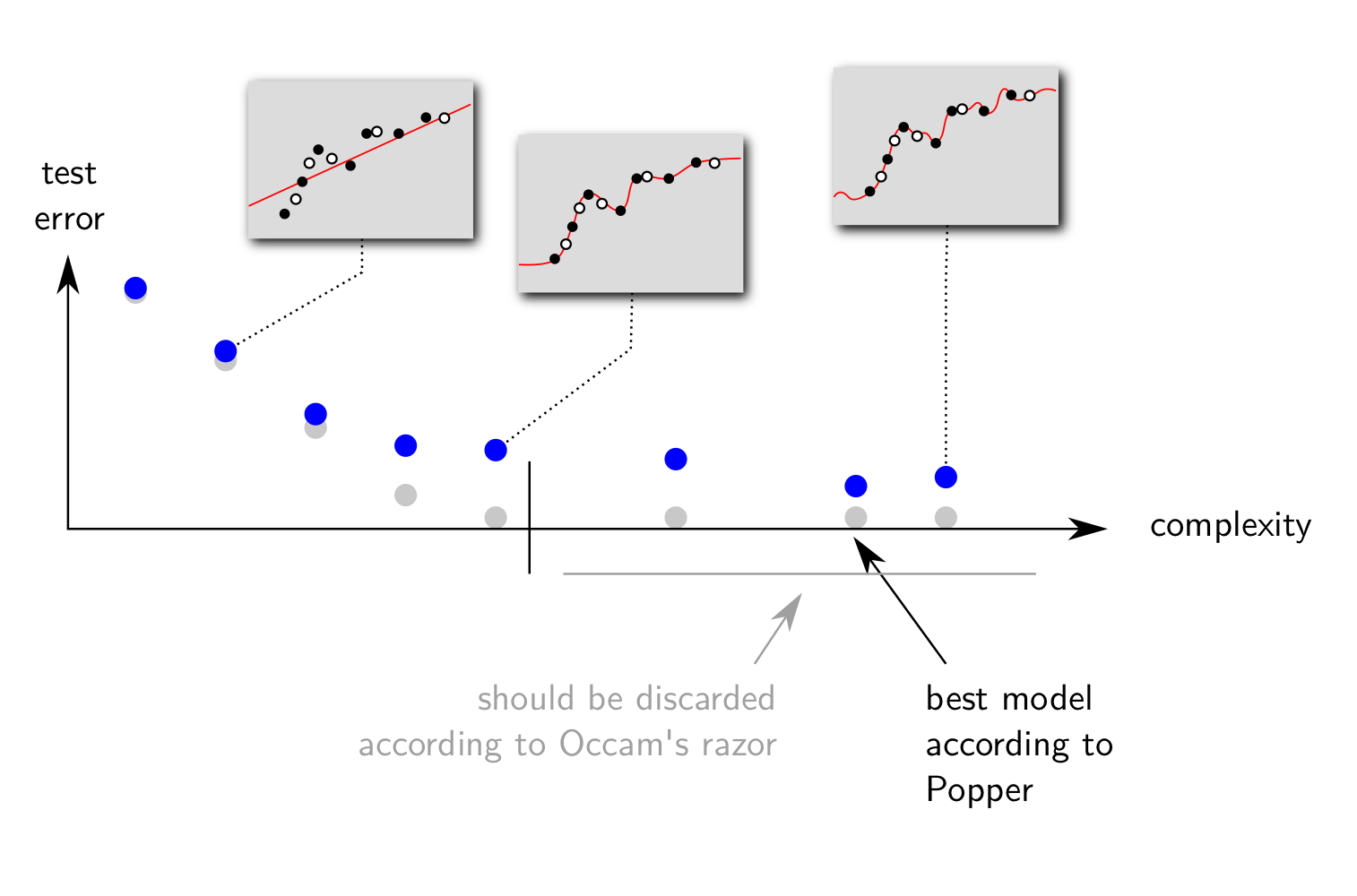
포퍼의 이론에 바탕한 모델 선택 예 1

포퍼의 이론에 바탕한 모델 선택 예 2

위처럼 모델의 복잡성에 대해서 학습 오차가 감소하는 반면 검정 오차가 증가하는 현상을 오버 피팅이라고 한다. 오버 피팅된 모델은 관찰된 데이터에 대해서만 좋은 성능을 가질 뿐, 앞으로 관찰할 데이터에 대해서는 오차가 크다. 따라서 오버 피팅이 되지 않은 좋은 모델을 선택하기 위해 학습 오차가 아닌 검정 오차가 가장 작은 모델을 선택한다.

---

초모수(Hyperparameter)

모수화된 가설 공간(Hypothesis Space) $\mathcal {H}_{\theta} = \{ h_{w, \theta}(x) | w \in \mathbb {R}^{k + 1} \}$에서 초모수를 $\theta = (\theta_1, \cdots, \theta_{l}) \in \mathcal {P}$라고 하자. 초모수란, 가설 공간 $\mathcal {H}_{\theta}$을 특정 학습 문제에 알맞게 조정하기 위해 사용되며, 주로 모델의 복잡도나 형태를 조율하는 역할을 한다.

---

예 1) 다항식

• $\theta = k =$ 다항식의 최고차항
• $w = (w_0, w_1, \cdots, w_k)$
• $h_{w, \theta}(x)$는 $k + 1$개의 구성 요소 $\phi_j (x) = x^j, j = 0, \cdots, k$를 갖는다.

  ---

예 2) 방사형 기저 함수

• $\theta = (k, \mu_1, \cdots, \mu_k, \sigma_1, \cdots, \sigma_k)$
• $w = (w_0, w_1, \cdots, w_k)$
• $h_{w, \theta}(x)$는 $k$개의 구성 요소 $\phi_j (x) = \exp (- \frac {|| x - \mu_j ||^2}{\sigma_j})$를 갖는다.

  ---

예 3) 정규화된 다항식

• $\theta = (k, \lambda)$
• $k =$ 다항식의 최고차항
• $\lambda =$ 정규화 모수(Regularization Parameter) 
• $w = (w_0, w_1, \cdots, w_k)$

---

홀드 아웃 검증(Holdout Validation) (데이터 양이 많을 때)

권장되는 데이터 집합 분리 비율

데이터 집합 $\mathcal {D} = (x_1, y_1), (x_2, y_2), \cdots, (x_r, y_r)$가 주어진다고 하자. 데이터 집합 $\mathcal {D}$을 임의로 세 개의 집합으로 분리(Split)한다.

• 학습 집합(Training Set): $$\mathcal {D}_{train} = (x_1, y_1), (x_2, y_2), \cdots, (x_m, y_m)$$
• 검증 집합(Validation Set): $$\mathcal {D}_{val} = (x^v_1, y^v_1), (x^v_2, y^v_2), \cdots, (x^v_p, y^v_p)$$
• 검정 집합 또는 홀드 아웃 세트(Test Set or Holdout Set): $$\mathcal {D}_{test} = (x^t_1, y^t_1), (x^t_2, y^t_2), \cdots, (x^t_q, y^t_q)$$

  ---

홀드 아웃 검증을 통한 모델 평가

아래와 같은 알고리즘을 통해 모든 초모수 $\theta \in \mathcal {P}$에 대하여 가설 $h^*_{\theta}$을 구하고 각 가설에 대한 검증 오차 $E_{val} [ h^*_{\theta}]$를 계산한다. 검증 오차가 가장 작은 가설 $h^* \in \{ h^*_{\theta} | \theta \in \mathcal {P} \}$을 선택 후, 검정 오차 $E_{test} [h*]$로 모델을 평가한다.

홀드 아웃 검증의 모델 평가 절차

※ 참고

$\mathcal {P}$	초모수 구성의 집합(Set of Hyperparameter Configurations)
$E_{train} [h]$	가설 $h$의 학습 오차(Training Error of Hypothesis $h$)
$E_{val} [h]$	가설 $h$의 검증 오차(Validation Error of Hypothesis $h$)
$E_{test} [h]$	가설 $h$의 검정 오차(Test Error of Hypothesis $h$)
$h^*_{\theta}$	모든 $h \in \mathcal {H}_{\theta}$에 대해서 $E_{train} [h]$를 최소화하는 가설(Minimizer of $E_{train} [h] \text { for all } h \in \mathcal {H}_{\theta}$)

---

홀드 아웃 검증을 통한 모델 평가 응용

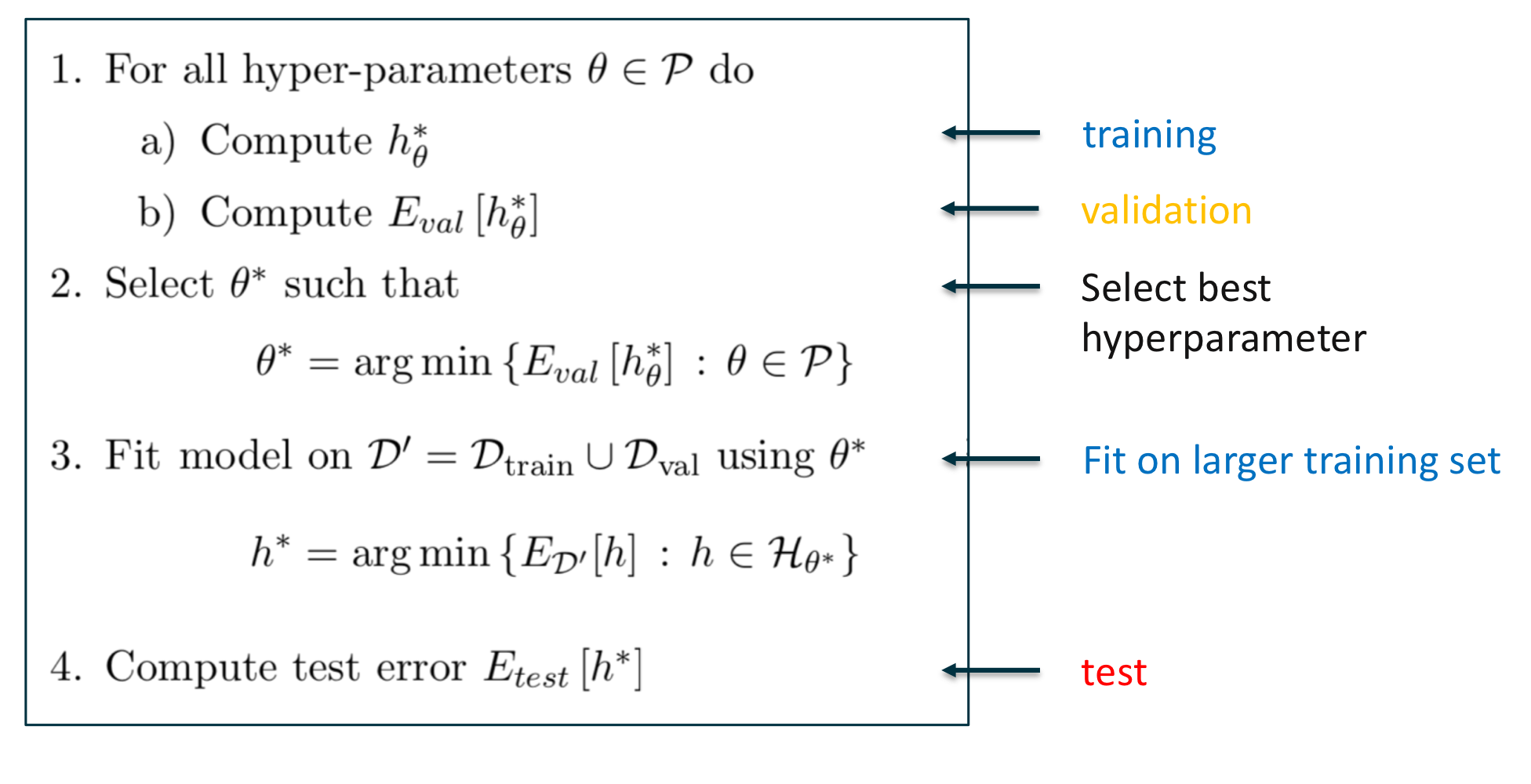
홀드 아웃 검증의 모델 평가 절차 응용

---

홀드 아웃 검증을 통한 모델 선택

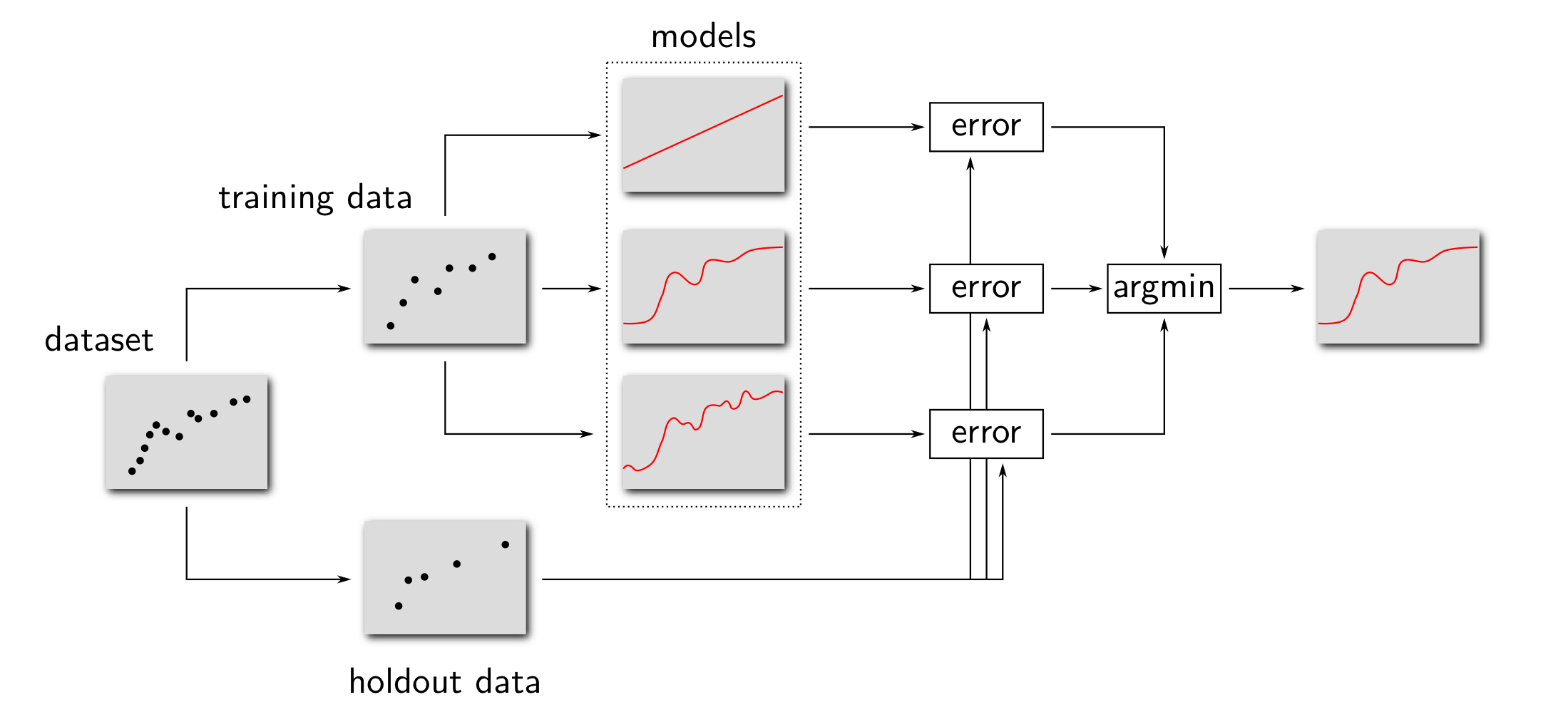
※ 검증 집합을 고려하지 않은 홀드 아웃 검증 알고리즘

---

홀드 아웃 검증의 세 가지 오차 비교

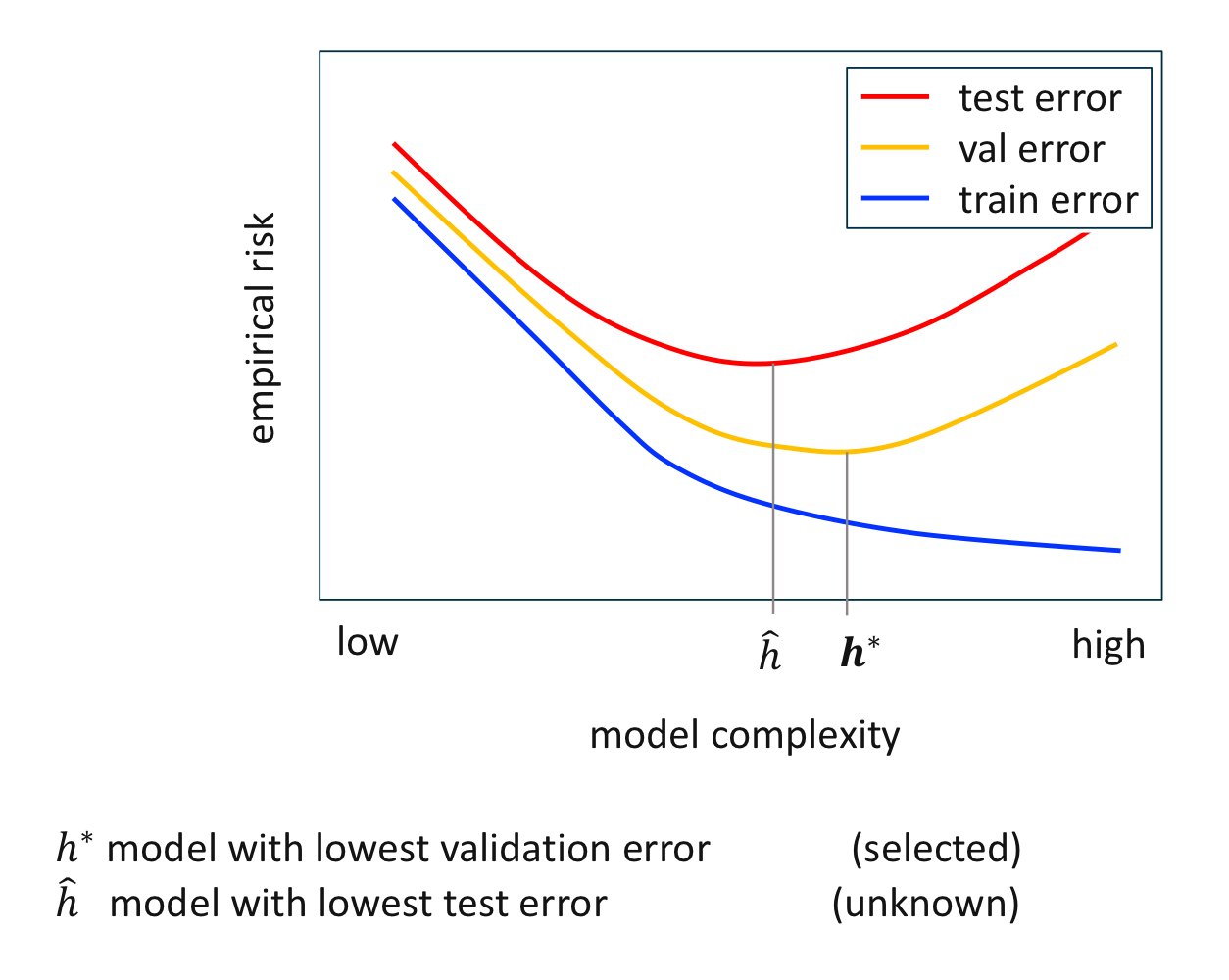
최저 검증 오차를 갖는 가설 $h^*$을 선택했을 때와 최저 검정 오차를 갖는 가설 $\hat {h}$에는 차이가 있다. 이 차이가 작을수록 아직 관찰되지 않은 데이터를 좀 더 정확하게 예측할 수 있으며, 따라서 더 좋은 모델로 간주한다.

---

K겹 교차 검증(K-Fold Cross Validation) (데이터의 양이 적을 때)

K겹 교차 검증은 데이터의 양이 적을 때 검증하는 기법으로 데이터의 여러 번 재사용해서 좀 더 좋은 모델을 선택한다. 

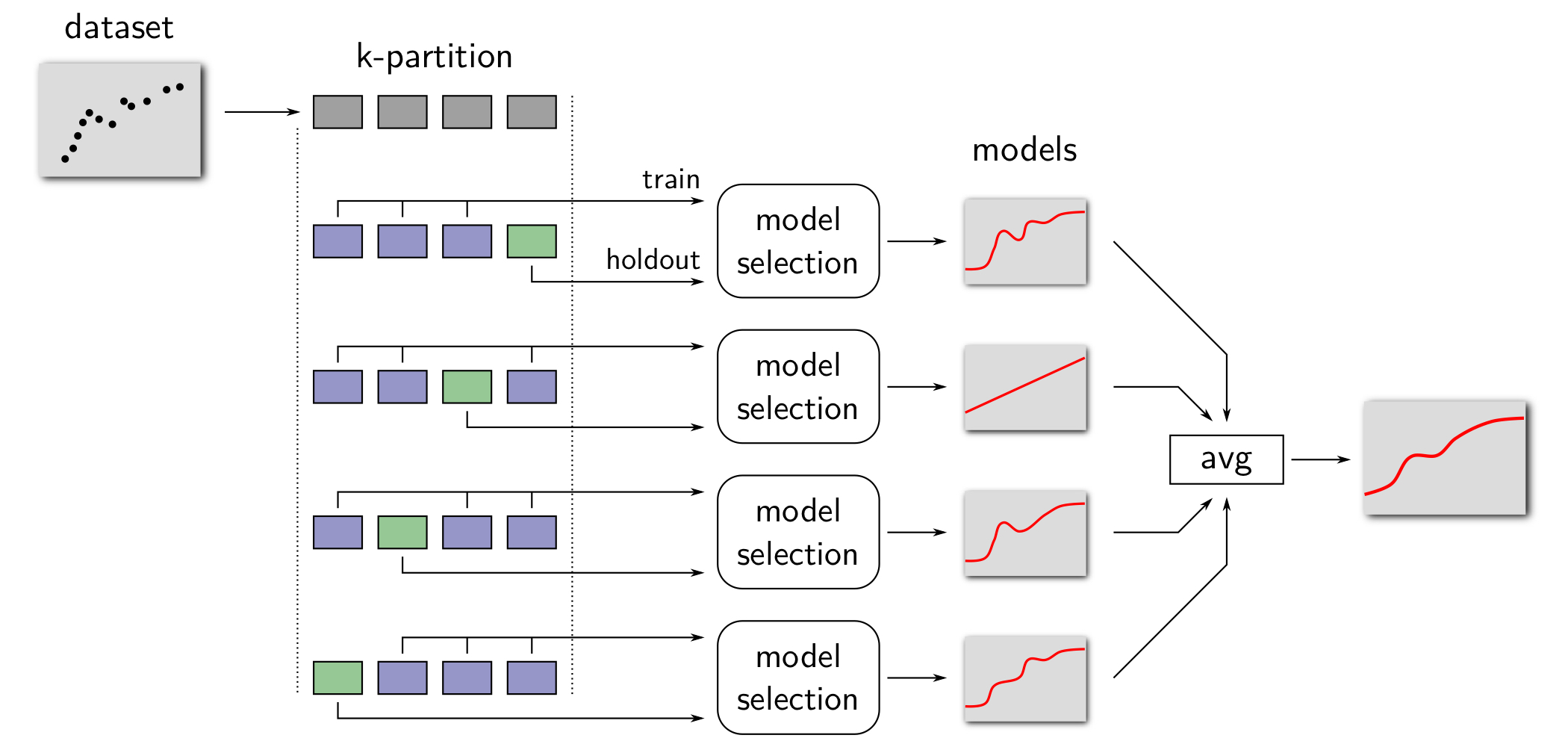
※ 검증 집합을 고려하지 않은 k겹 교차 검증 알고리즘

데이터 집합 $\mathcal {D} = (x_1, y_1), (x_2, y_2), \cdots, (x_r, y_r)$가 주어진다고 하자. 일반적인 모델 선택의 절차를 따라 데이터를 분리하면 각 집합에 속하는 데이터의 양이 현저히 작을 뿐만이 아니라 각 집합의 원래 목적을 달성하는 데 어려움이 있다. 따라서 데이터 집합을 세 개의 집합이 아니라 $K$개의 부분 집합(Subset) $\mathcal {D}_1, \cdots, \mathcal {D}_K$로 분리한다. 

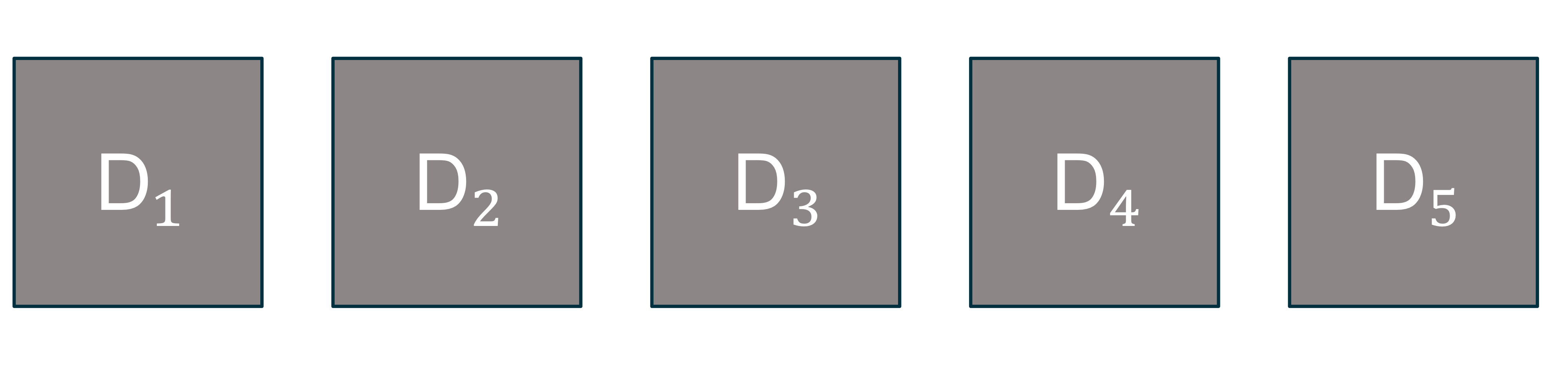
5겹 교차 검증의 데이터 분리 초기 상태

총 $K$번의 반복을 통해 학습 집합과 검정 집합을 매번 다르게 설정한다. 이때, 학습과 검정 집합의 비율은 4:1가 널리 사용되고 있다.

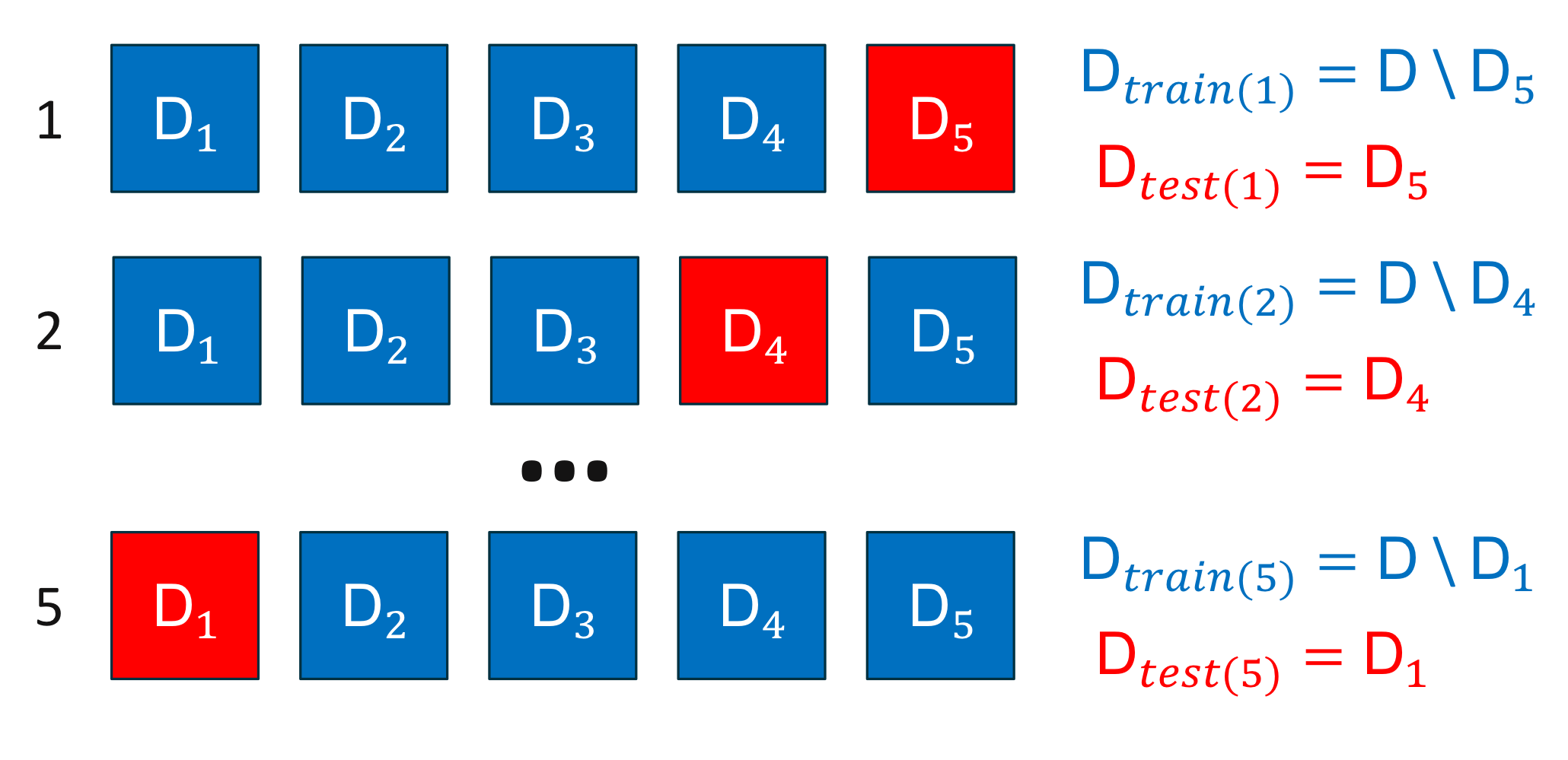
5겹 교차 검증의 학습, 검정 데이터 분리

---

K겹 교차 검증을 통한 모델 평가

$K$개의 데이터 세트 $\mathcal {D}_1, \cdots, \mathcal {D}_K$에 대하여 각각 가장 작은 검정 오차를 갖는 모델을 선택한 후, $K$개의 모델 중 다시 가장 작은 검정 오차를 갖는 모델을 선택하거나 모델의 평균을 구하여 최종 모델을 평가한다. 아래의 알고리즘은 가장 작은 검정 오차를 갖는 모델을 평가하는 K겹 교차 검증의 모델 평가 절차를 나타낸다. 

K겹 교차 검증의 모델 평가

※ 참고

$CV_K$

$K$개의 모델의 평균 검증 오차(Average Test Error of $K$ Selected Models)

---

K겹 교차 검증을 통한 모델 선택

K겹 교차 검증의 모델 선택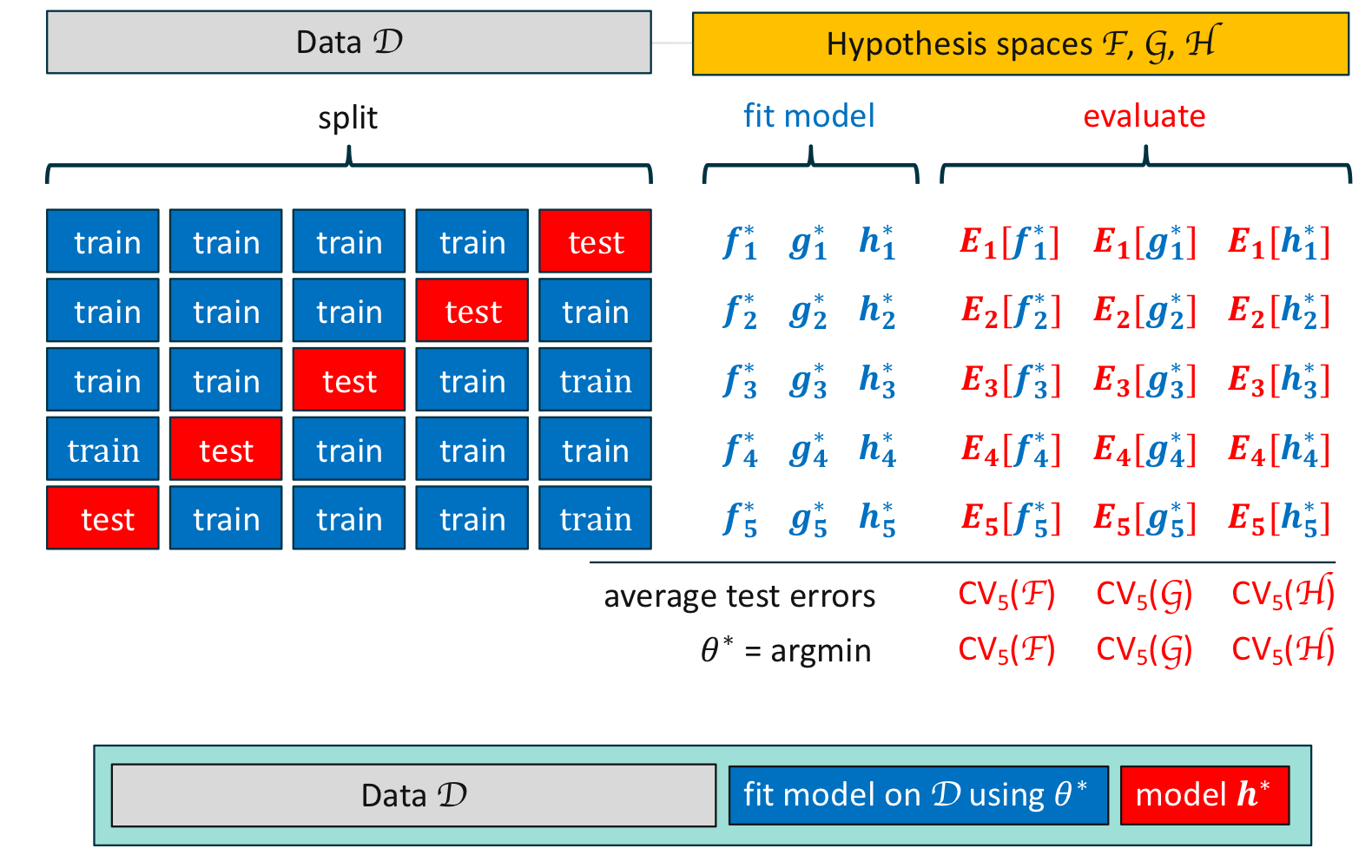

K겹 교차 검증의 모델 선택의 예 1

---

홀드 아웃 검증과 K겹 교차 검증의 비교(Comparison of Holdout and K-Fold Cross Validation)

• 홀드 아웃 검증과 K겹 교차 검증은 아직 관찰되지 않은 데이터를 잘 예측할 수 있는 모델을 목표로 한다.
• 관찰된 데이터 내에서 검증을 하는 방법으로 주어지는 데이터가 타당한지 따져야 한다.
• 데이터를 분리할 때, 학습 데이터의 비율을 감소시키면 부정확한 모델을 생성하기 쉽고, 그 반대로 비율을 증가시키면 알고리즘이 계산적으로 비싸진다.

---

중첩 교차 검증(Nested Cross Validation)

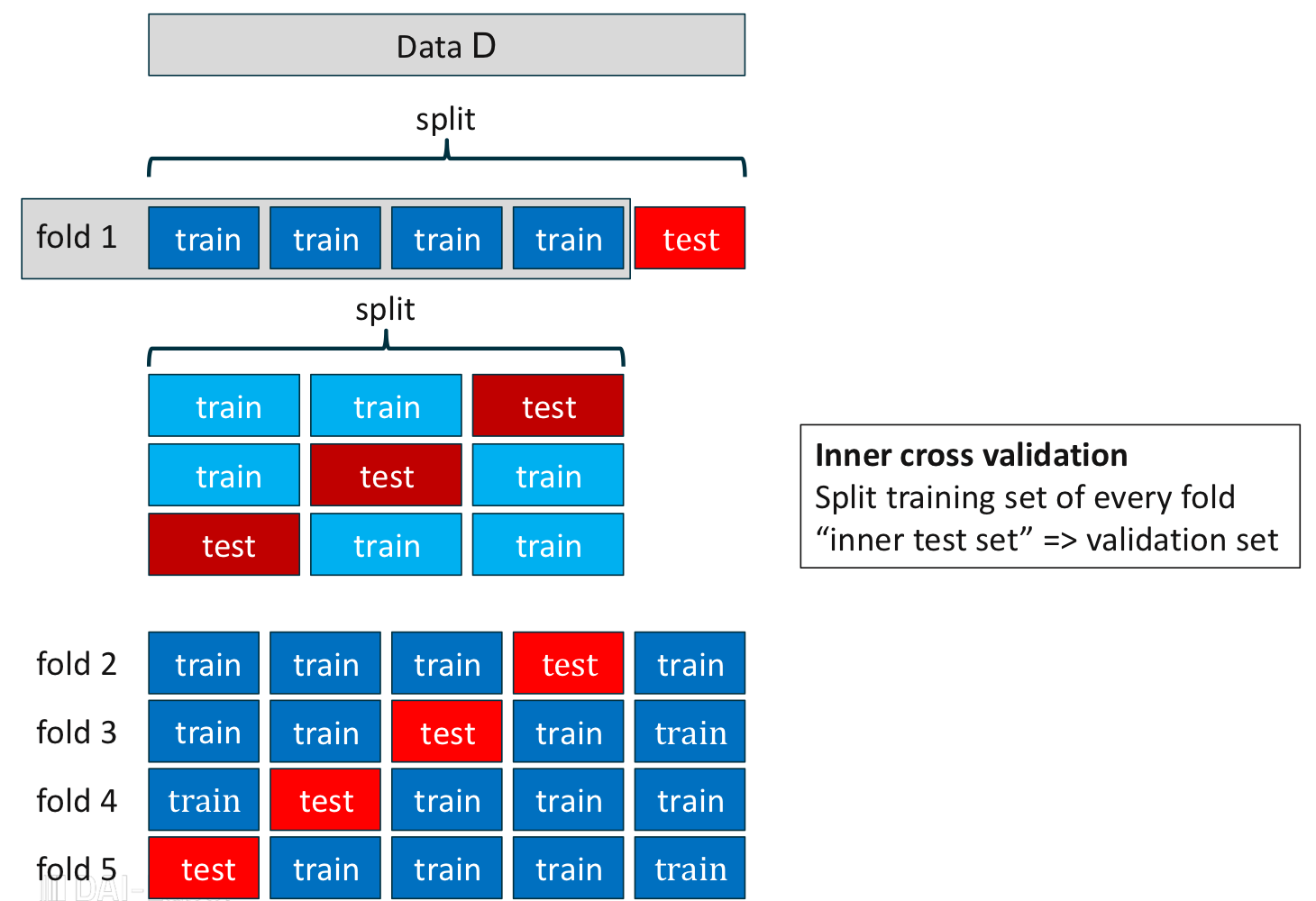
중첩 교차 검증의 데이터 분리

K겹 교차 검증에서 각 반복에서 할당했던 학습 집합을 또다시 $L$개의 부분 집합으로 나누어 그중 일부분을 학습 집합과 검정 집합으로 분리한다.

---

중첩 교차 검증을 통한 모델 평가

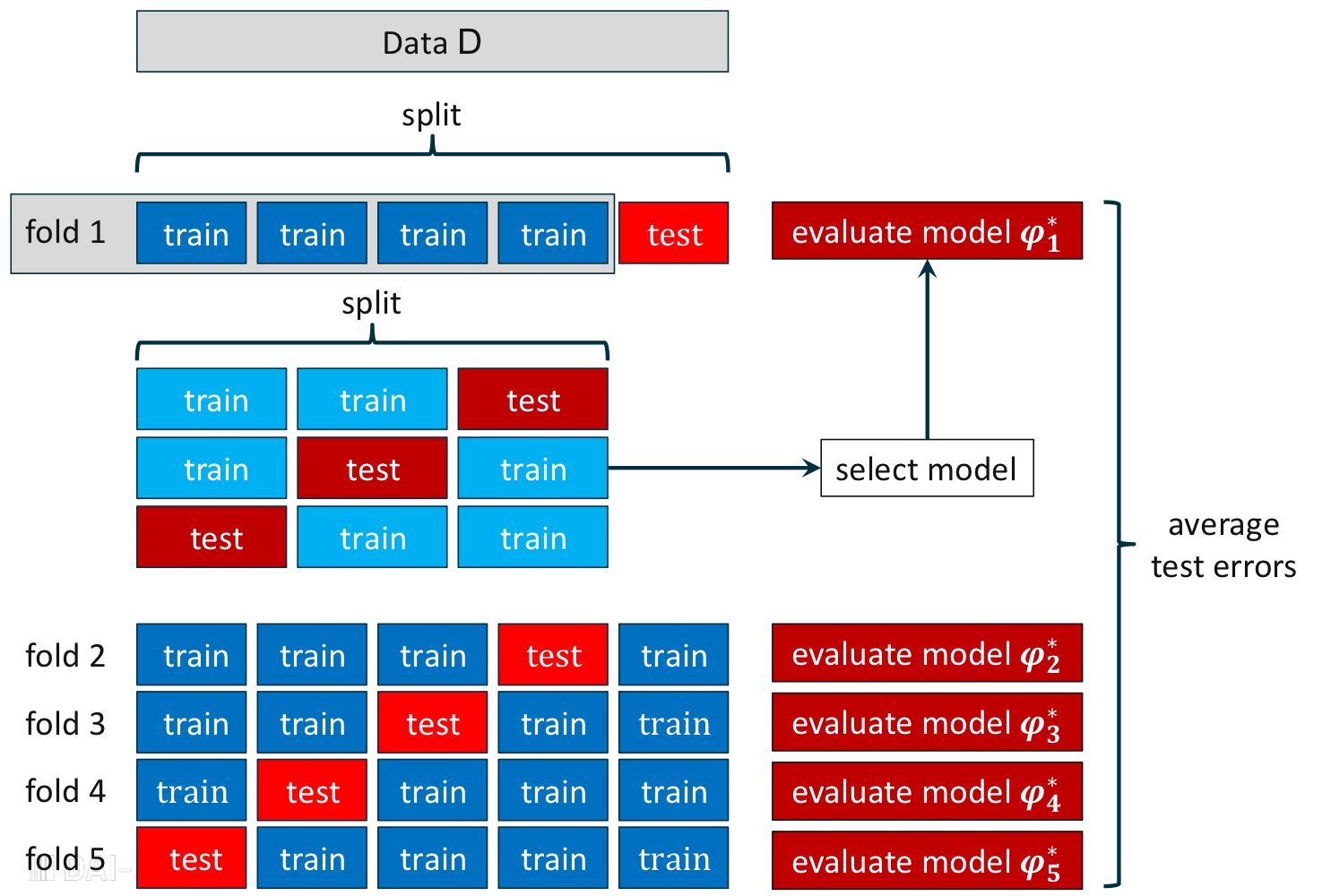
 한정된 데이터로 반복적으로, 중첩적으로 모델을 선발한 후, 최종적으로 평균 검정 오차를 계산하여 일반화 오차를 예측할 수 있다. 

중첩 교차 검증의 모델 평가 절차

---

중첩 교차 검증을 통한 모델 선택

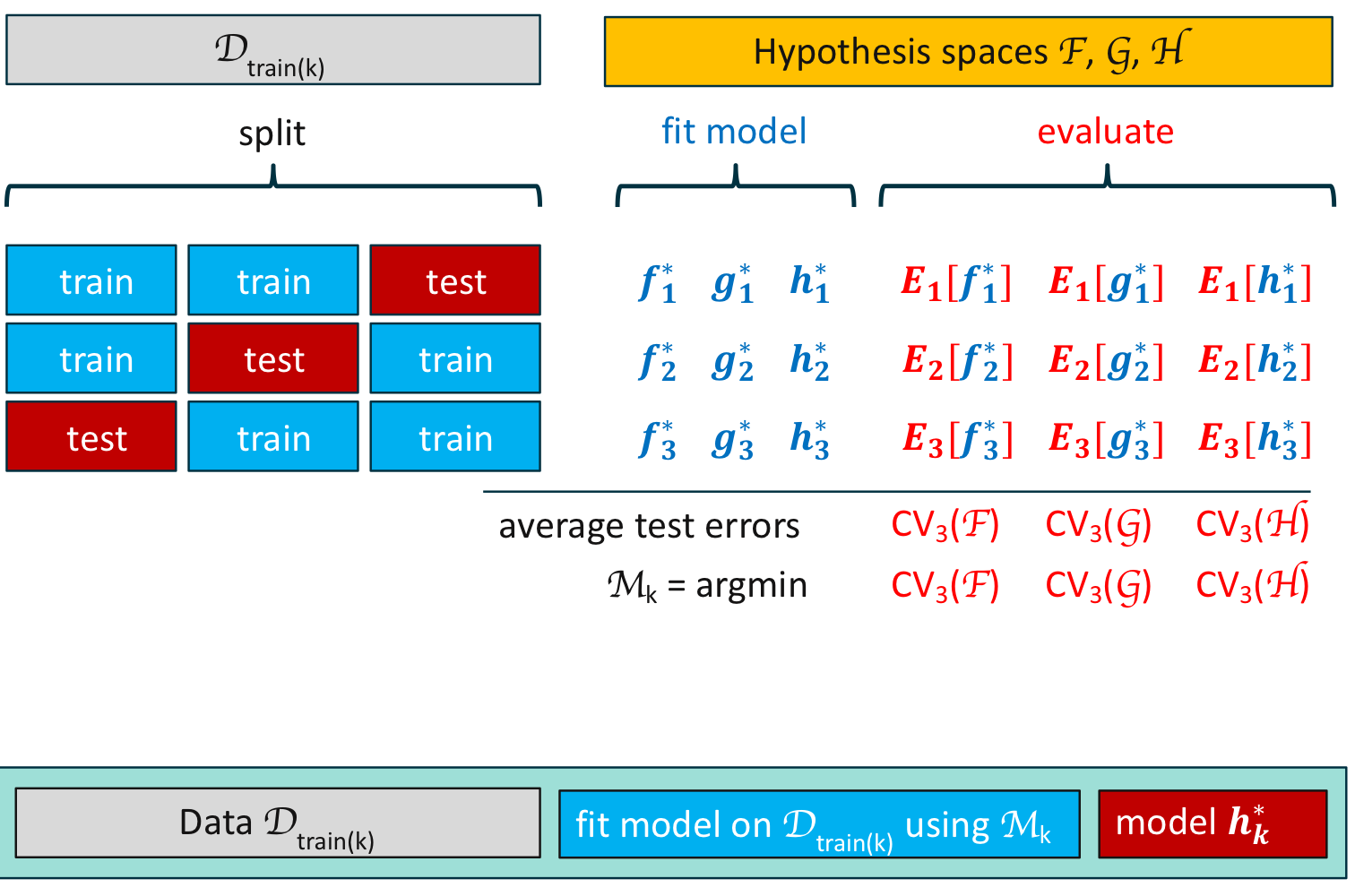
중첩 교차 검증의 모델 평가의 예 1

각 가설 공간에 대해서 최소의 검정 오차를 갖는 최적의 가설을 구하여 최적의 가설 공간을 선택한다.

---

1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.

2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.