-
[Machine Learning] 언더 피팅과 오버 피팅(Underfitting and Overfitting)Informatik 2022. 2. 12. 05:21반응형
일반적으로 학습 데이터는 실제 데이터의 부분 집합이므로 학습 데이터에 대해서 오차가 감소하지만 실제 데이터에 대해서 오차가 증가하는데, 이 현상을 오버 피팅이라고 부른다. [wikipedia]
$m$개의 학습 데이터(Training Data) 세트가 주어졌을 때, 미지수의 매핑 함수(Mapping Function) $f: \mathbb {R}^n \rightarrow \mathbb {R}$를 가장 알맞게 예측해보자.
- 가설 공간(Hypothesis Space) $\mathcal {H}$을 정한다.
- 경험적 위험도(Empirical Risk) $E_m [h]$를 최소화한다. (※ ERM 자료)
- ERM으로 미지수 함수 $f$를 예측한다.
이제 F를 함수 $h: \mathbb {R}^n \rightarrow \mathbb {R}$의 집합이라고 하고, G $\subseteq$ H $\subseteq$ F를 만족하는 G, H를 가설 공간이라고 하자. $k < n$에 대해서 G $= \mathcal {H}_k$를 k차 다항식, H $= \mathcal {H}_n$를 n차 다항식을 지칭할 때, 가설 공간 H 대신 G를 선택해야 할 경우가 있을까? 이에 대한 답은 오버 피팅에 대해 다루면서 설명하겠다.
미지수의 데이터 분포 $p(x, y)$를 따르는 레이블의 샘플 데이터 $(x_1, y_1),..., (x_N, y_N)$를 가정할 때, 머신러닝에서는 관찰되었던 데이터 $x_1,..., x_N$을 잘 예측할 뿐만 아니라, 데이터 분포 $p(x)$를 따르는 관찰되지 않은 데이터까지도 알맞게 레이블링을 할 수 있는 모델 $f(x)$를 구하고자 한다.
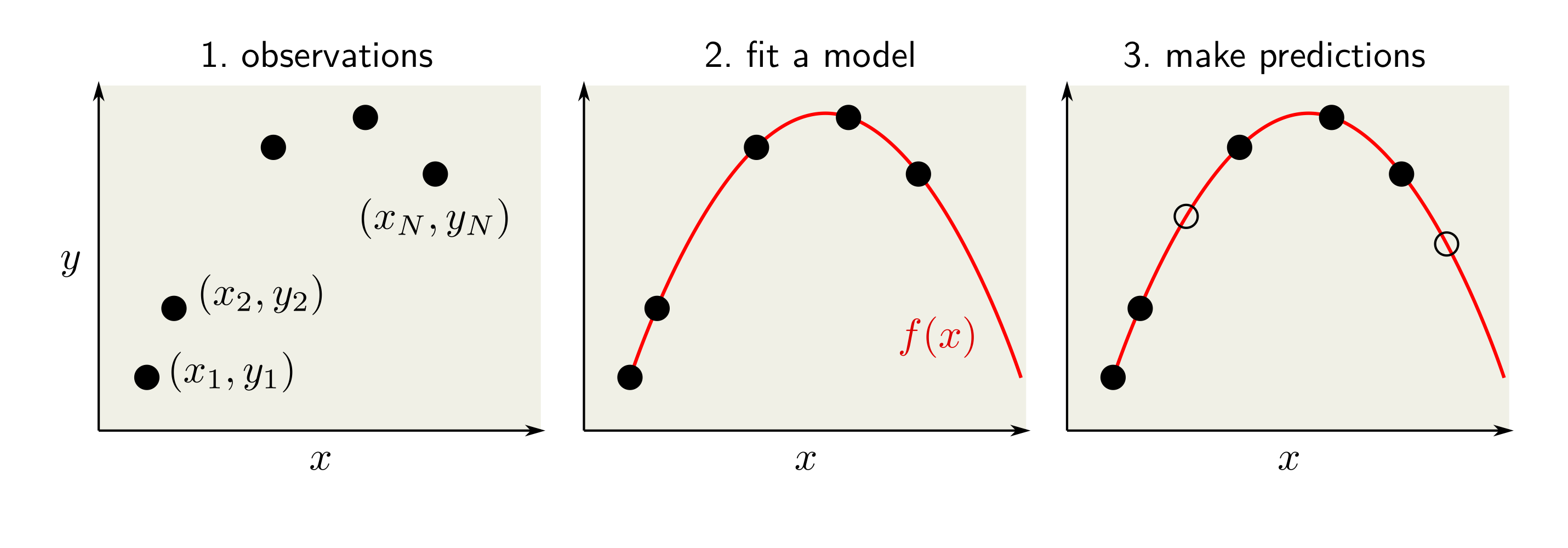
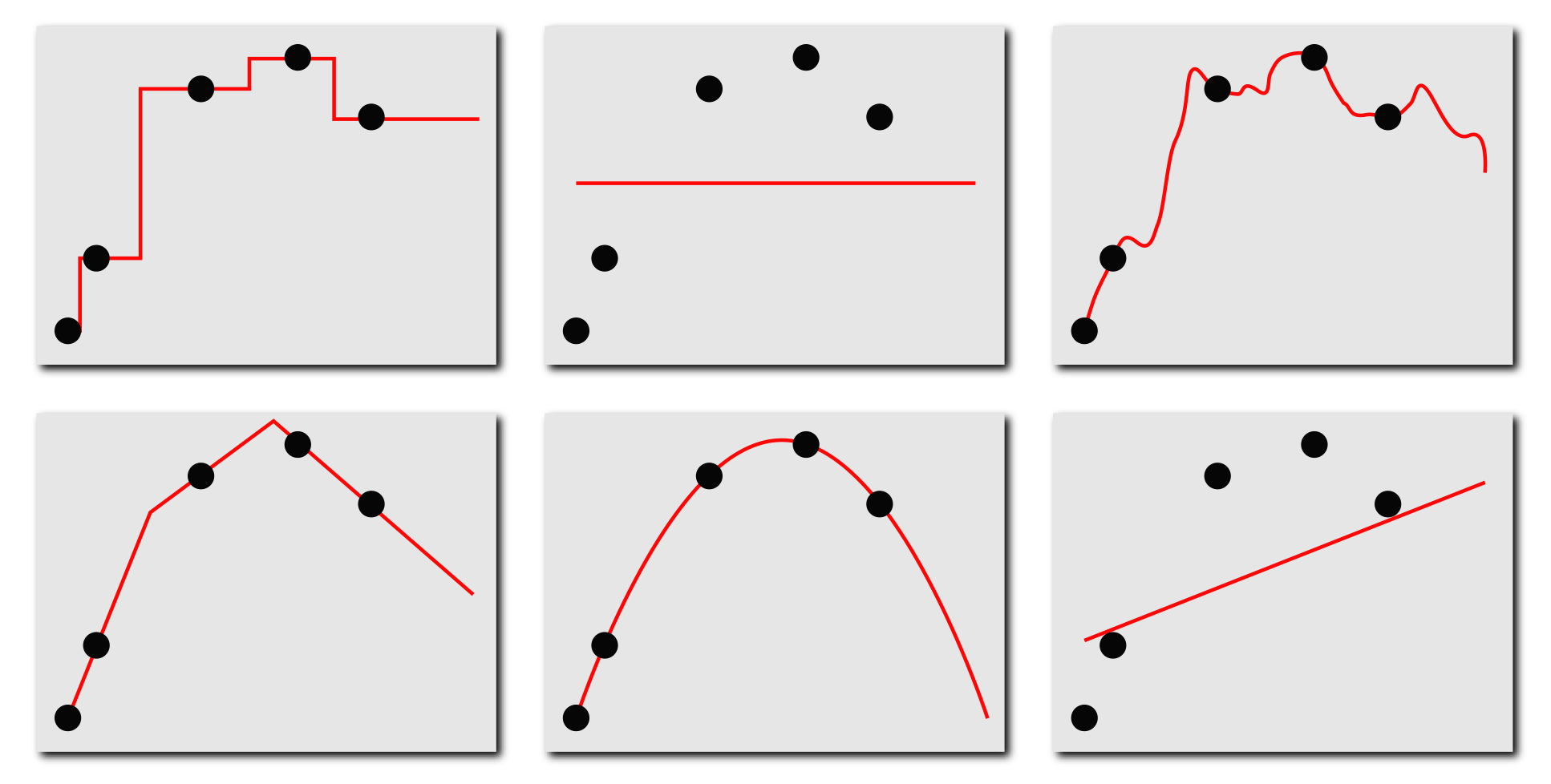
머신러닝의 기본적인 절차 예를 들어, 아래의 그림처럼 머신러닝으로 다양한 모델들을 학습할 수가 있는데, 어떻게 좋은 모델을 학습할 것인지 고려해봐야 한다. 어떤 모델이 데이터를 잘 예측하는 가? 모델이 관찰된 데이터를 완벽하게 예측해야 할까? 관찰된 데이터를 완벽하게 예측할 수 있다면 어떤 문제가 발생할까? 등의 질문들의 답이 모델 선택하는 데에 있어서 기준점이 될 수 있다.
오캄의 면도날(Occam's Razor) 법칙:
"Entities must not be multiplied beyond necessity." [William of Ockham (1287-1347)]
오캄의 면도날 법칙에 의하면 머신러닝에서 데이터를 올바르게 예측할 수 만 있다면 굳이 모델의 복잡성(Model Complexity)을 증가시킬 필요가 없다. 예를 들어, 노이즈(Noise)가 존재하는 함수 $f$으로부터 데이터가 생성되었다고 가정하자. 관찰된 데이터는 완벽한 함수 모양을 따르지 않고 어느 정도 오차가 있는 형태를 띨 것이다. 따라서, 학습 오차(Training Error)가 매우 작은 모델을 선택한다는 것은 실제 데이터의 성질을 제대로 담지 못하고, 관찰된 데이터에 대해서만 과하게 학습하게 됐음을 뜻한다. 아래의 그림에서 확인할 수 있듯이, 관찰 데이터를 완벽하게 훈련할수록 모델의 복잡성은 증가하며, 이에 따라 학습 오차는 매우 작게 측정된다. 하지만, 머신러닝에서는 관찰된 데이터만 잘 예측하는 것이 아니라 데이터의 노이즈까지 고려해 미래의 데이터까지 잘 예측할 수 있는 모델을 지향하므로 이미 데이터의 예측이 가능하다면 불필요하게 모델을 복잡하게 구성할 필요가 없다는 결론에 다다를 수 있다.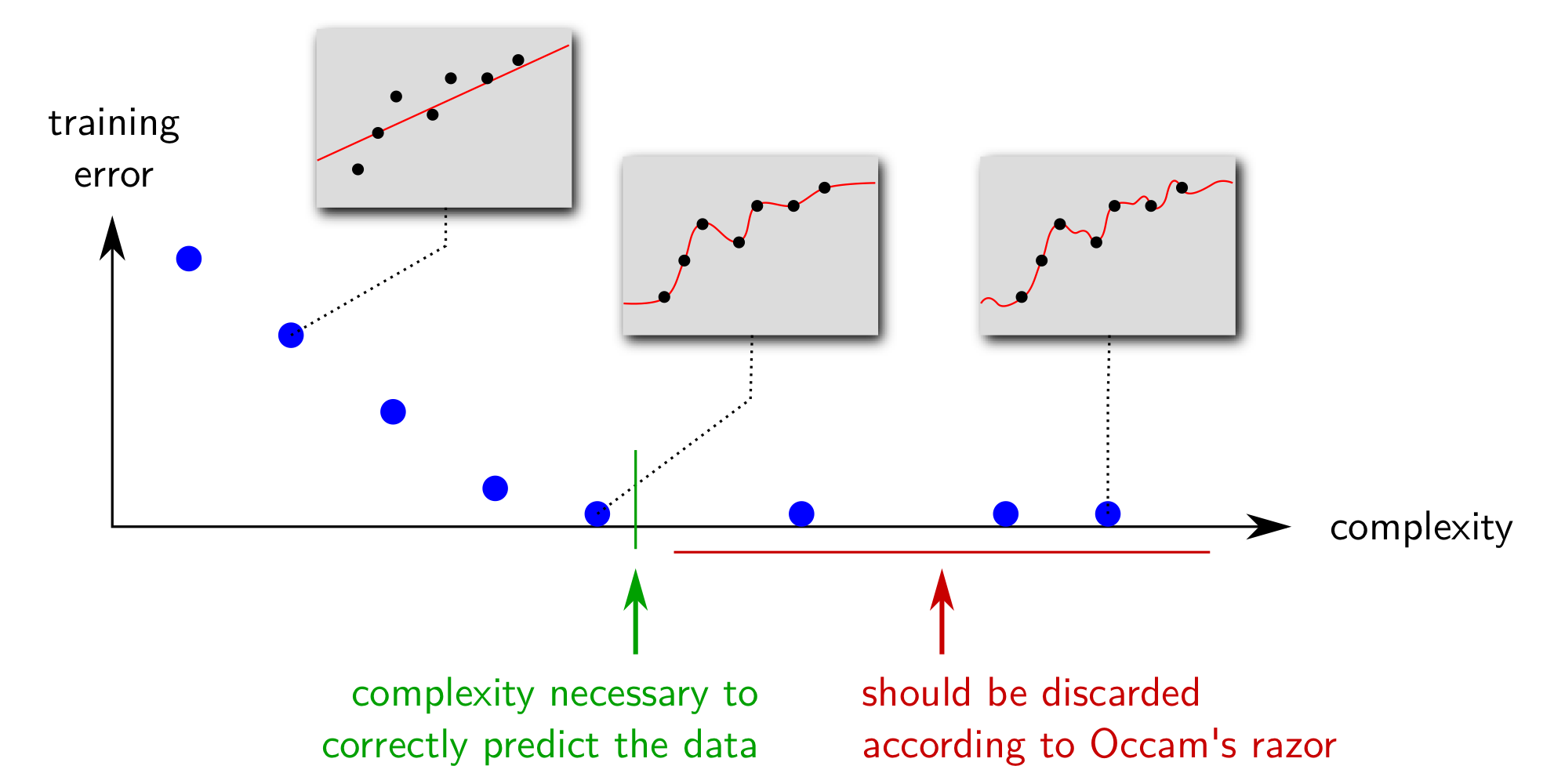
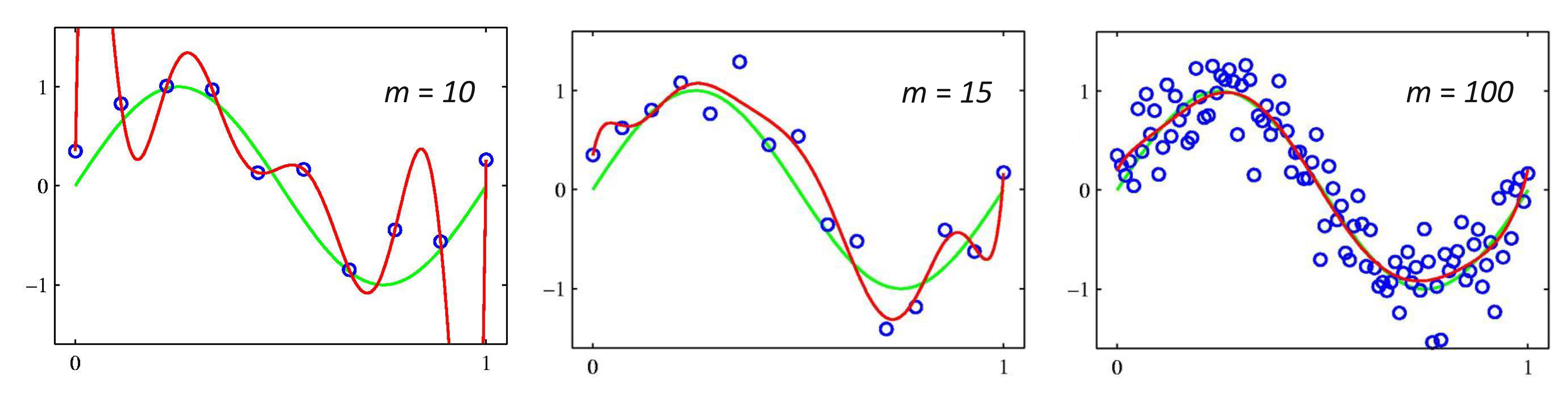
[해결 방안 ①] 학습 데이터의 양 늘리기
간단한 해결 방안으로 학습 데이터를 늘리는 방법이 있긴 하지만 한정된 데이터에서 학습을 해야 하는 경우에는 가능한 선택지가 아니다.
[해결 방안 ②] 정규화(Regularization)
또 다른 해결 방안으로, ERM에서 새로운 모수 $\lambda$로 일반적인 경험적 위험도 대신 정규화된 경험적 위험도를 사용한다.
$$E_m [h_w, \lambda] = E_m [h_w] + \lambda \Omega(h_w)$$
새로 추가된 $\lambda \Omega(h_w)$는 $w_j$가 매우 큰 값을 도달하지 않도록 제한해주는 역할을 한다.
예 1) 정규화된 MSE = L2 = 능형 회귀(Ridge Regression)
MSE(Mean Squared Error):
$$MSE = \frac {1}{n} \sum^n_{i = 1} (h(\mathbf {x}) - y)^2$$
L2는 일반적인 MSE에 정규화 역할을 담당하는 항을 추가한다.$$E_m [ h_w, \lambda ] = \frac { 1 }{ 2m } \sum^{m}_{i = 1} ( h_w(x_i) - y_i)^2 + \frac {\lambda}{2m} \sum^{n}_{i = 1} w_i^2$$
경사 하강법(Gradient Descent):
해당 식을 종료 시까지 반복
$$w_j \leftarrow w_j - \eta \frac {\partial}{\partial w_j} J(\mathbf {w}) \text { for all } j$$
이에 따라 경사 하강법(Gradient Descent)도 다음과 같이 바뀐다.해당 식을 종료 시까지 반복
$$w_0 \leftarrow w_0 - \eta \frac {1}{m} \sum^{m}_{i = 1} (h_w(x_i) - y_i) x_{i0}$$
$$w_1 \leftarrow w_1 - \eta \left ( \frac {1}{m} \sum^{m}_{i = 1} (h_w(x_i) - y_i) x_{i1} + \frac {\lambda}{m} w_1 \right )$$
$$\vdots$$
$$w_n \leftarrow w_n - \eta \left ( \frac {1}{m} \sum^{m}_{i = 1} (h_w(x_i) - y_i) x_{in} + \frac {\lambda}{m} w_n \right )$$
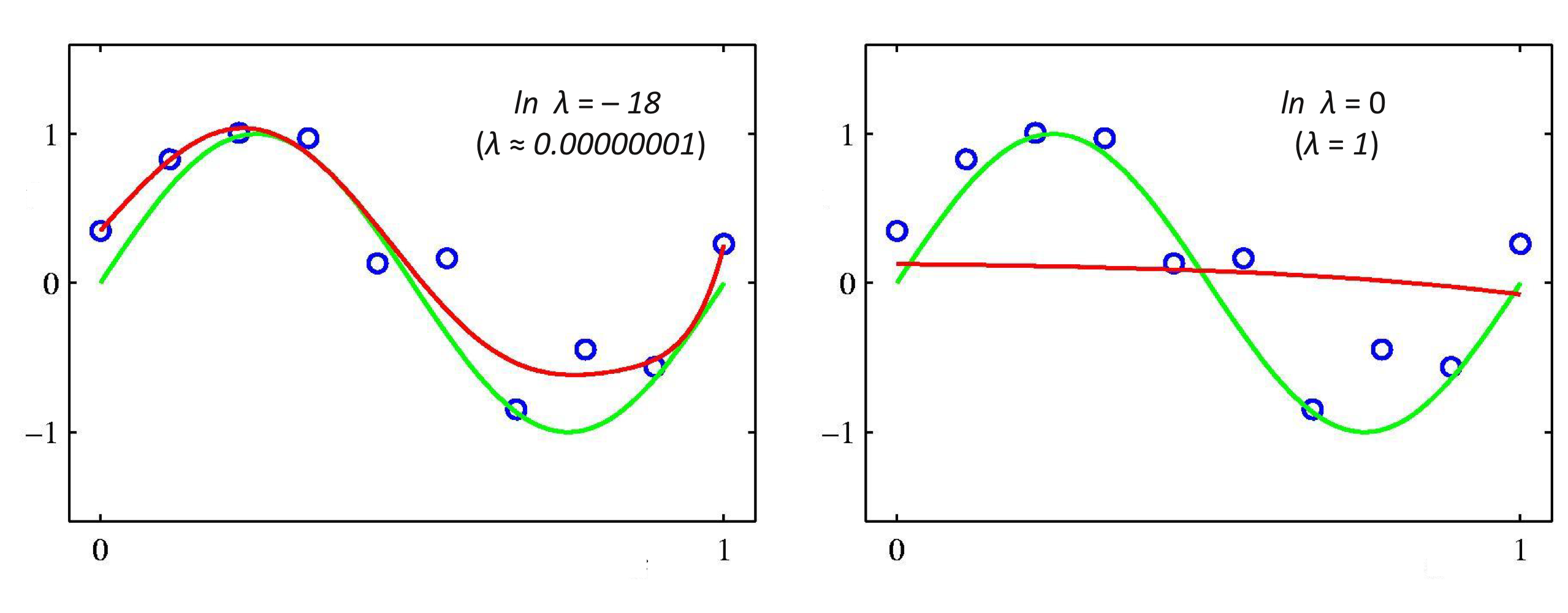
9차 다항식 모델에서 두 개의 다른 정규화 모수 $\lambda$로 달라지는 학습 모델 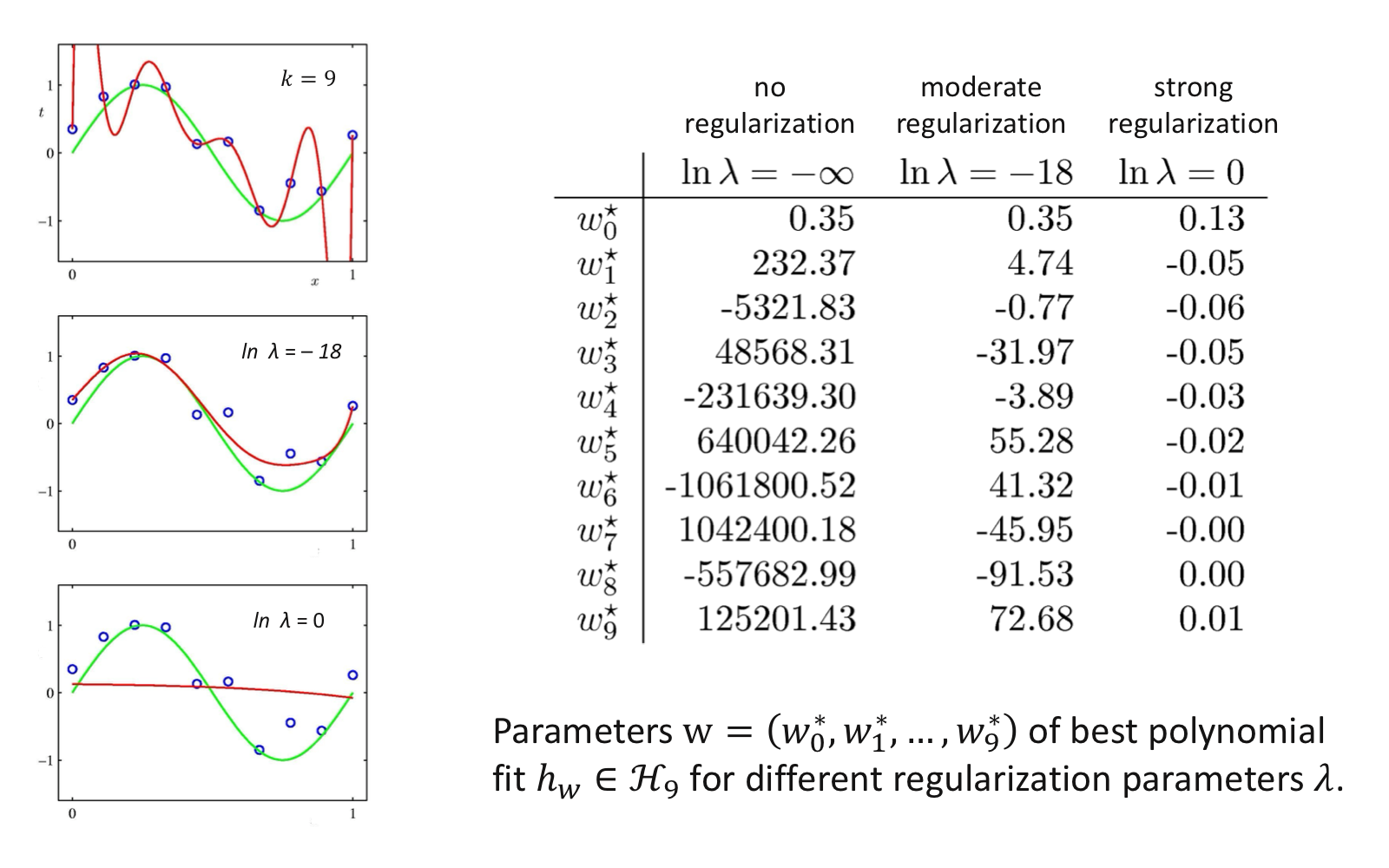
정규화 모수 $\lambda$에 따라 제한되는 $\mathbf {w}$의 크기 범위
[해결 방안 ③] 모델의 모수 개수 세기
모델의 복잡도를 한정하기 위해 후보 모델에서 각 사용되는 모수의 개수를 센 후, 가장 작은 모수를 사용하는 모델을 사용한다.

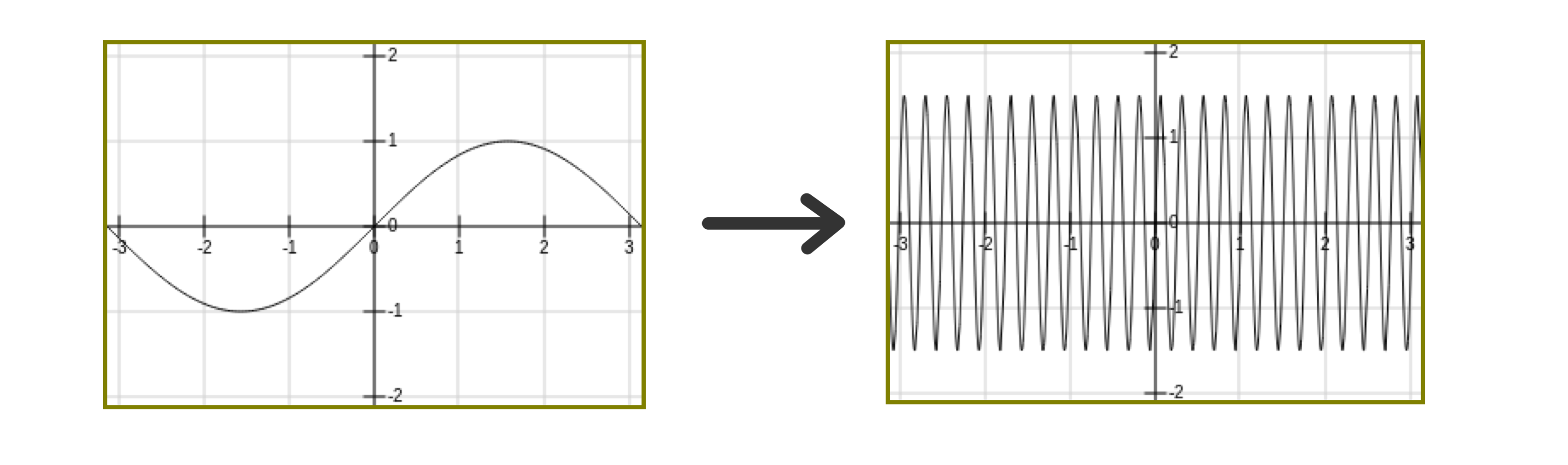
하지만 모든 모델의 복잡성이 단순히 모수의 개수에 영향받지는 않는다. 예를 들어, 아래와 같은 모델 $g(x) = a \sin(wx)$는 $a$와 $w$ 단 두 개의 모수를 가지지만 모수 설정에 따라 실수 상의 거의 모든 데이터도 피팅하는 오버 피팅의 모델이 될 수 있다.
[해결 방안 ④] 구조적 위험 최소화(Structural Risk Minimization)
SRM의 기본적인 개념은 다음과 같다.
해결하고자 하는 문제의 솔루션을 단계적으로 증가하는 형태의 집합 공간으로 구조화 → 만약 첫 두 개의 솔루션이 데이터를 잘 예측한다면, 그중 더 작은 집합 공간을 갖는 솔루션을 선택한다.
예 1) SRM
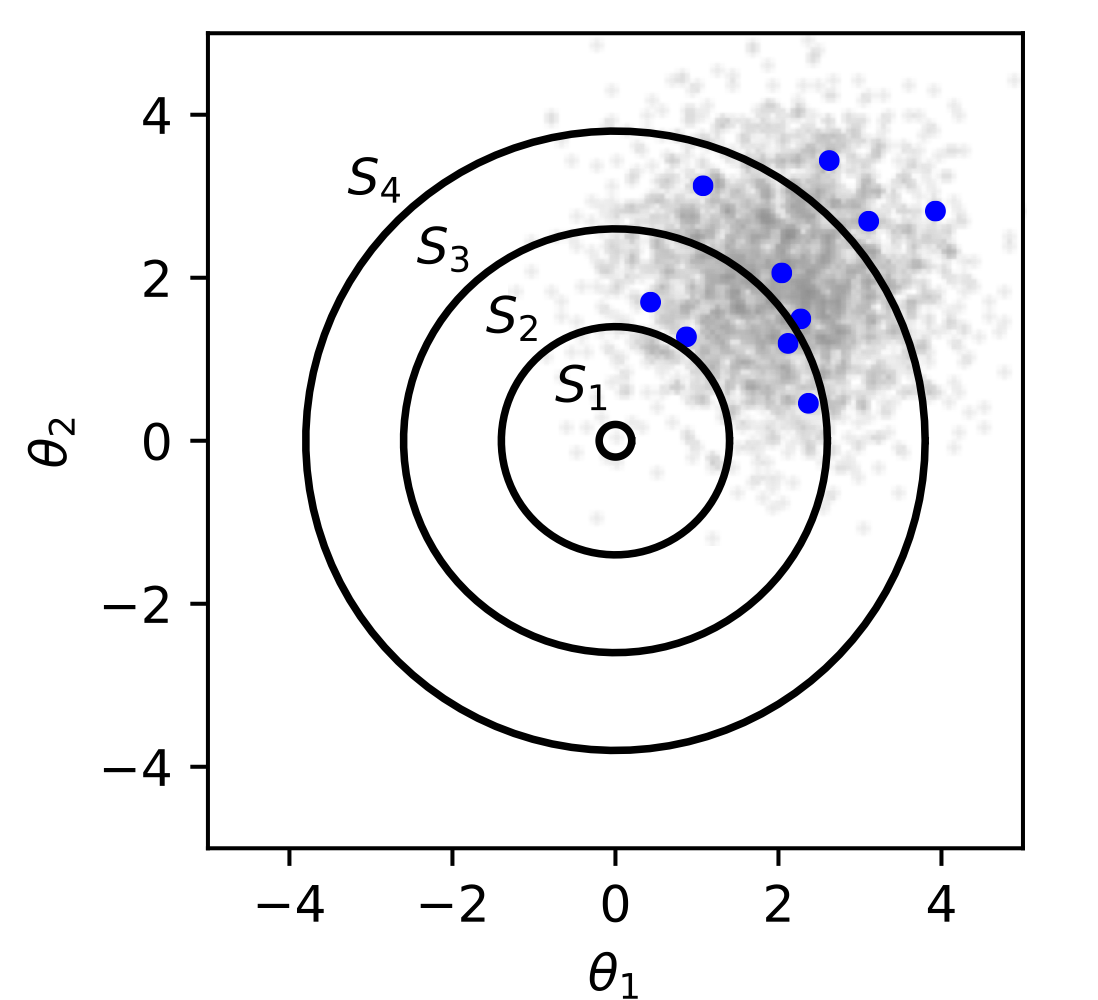
학습 데이터 $\mathbf {x}_1, ..., \mathbf {x}_N \in \mathbb {R}^d$가 독립적으로 어떤 분포에 의해 생성되었을 때, 이 분포의 평균값 $\mu \in \mathbb {R}^d$에 가장 가까운 MLE $\hat {\mu}$를 예측하자.
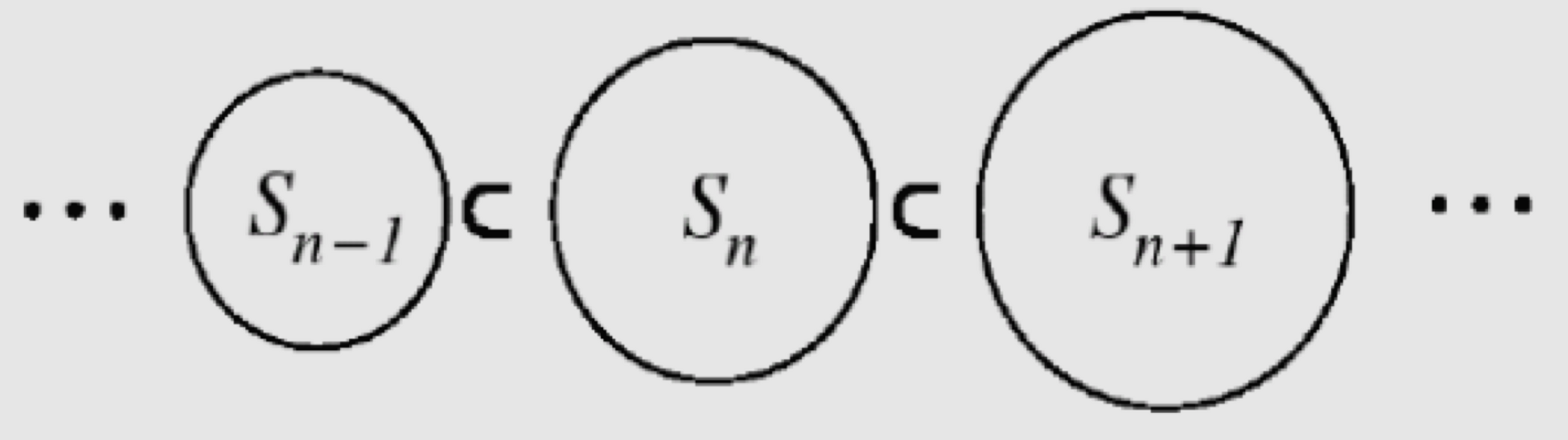
SRM 원칙을 적용하기 위해서는 우선 다음과 같은 집합 공간을 설립해야 한다.
$$\cdots \subseteq S_{n - 1} \subseteq S_{n} \subseteq S_{n + 1} \subseteq \cdots$$ $$\text {where } S_n = {\theta \in \mathbb {R}^d: ||\theta|| \leq C_n}$$
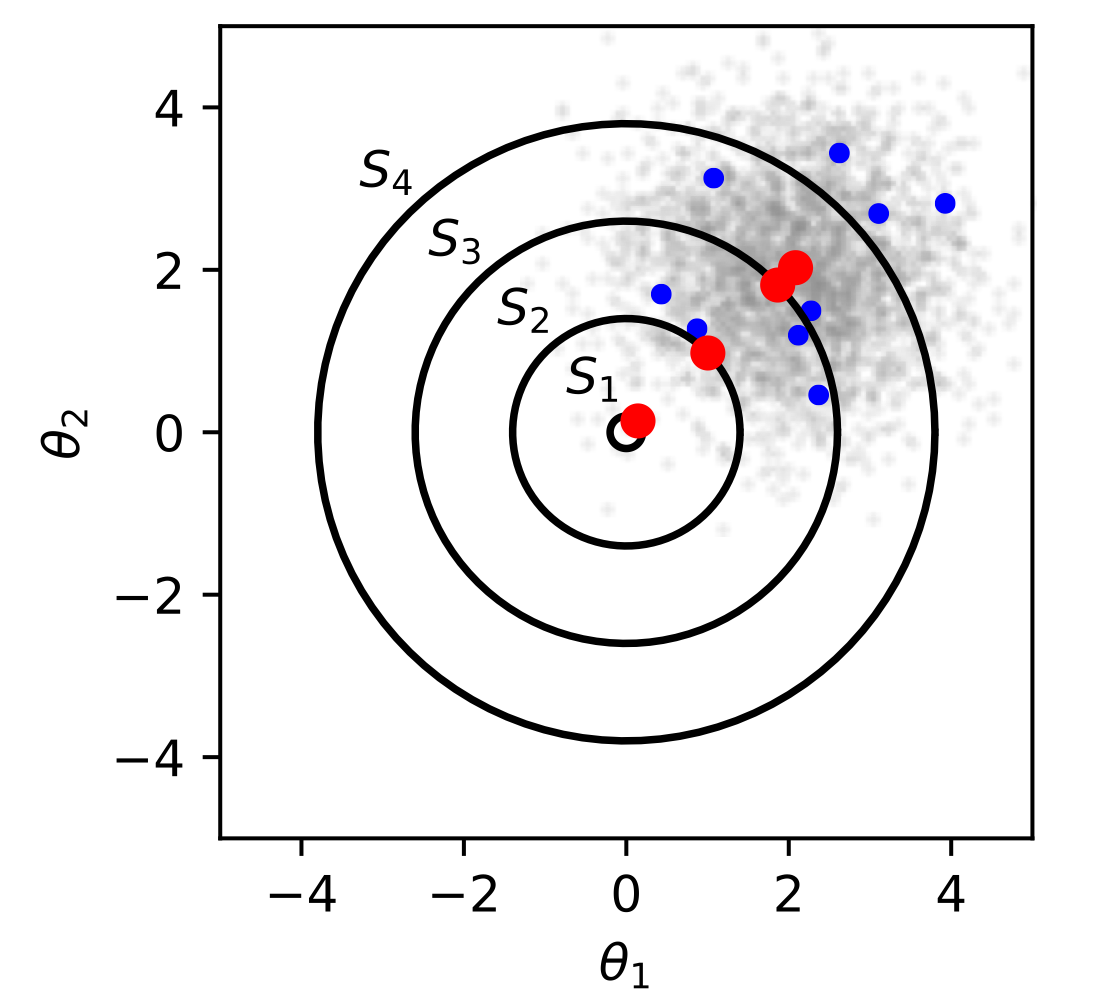
집합 공간 $S_n$에 해당하는 $\hat {\mu}$는 다음과 같이 계산할 수 있다. (두 번 째 그림에서의 빨간 점에 해당)
$$\hat {\mu} = arg \min_{\theta} \sum^{N}_{i = 1} || \theta - \mathbf {x}_i || \ \ \ \text {s.t. } \theta \in S_n$$
더 작은 집합 공간에 해당하는 $\hat {\mu}$가 실제 값 $\mu$에 더 가깝다.
※ [Machine Learning] 모델 평가와 선택(Model Assessment and Selection)
[Machine Learning] 모델 평가와 선택(Model Assessment and Selection)
※ 모델 선택에 있어서 중요한 개념: [Machine Learning] 오버 피팅(Overfitting) [Machine Learning] 오버 피팅(Overfitting) 일반적으로 학습 데이터는 실제 데이터의 부분 집합이므로 학습 데이터에 대해서 오..
minicokr.com
1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.
2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.
반응형'Informatik' 카테고리의 다른 글
[Machine Learning] 제임스-스타인 추정량(James-Stein Estimator) (0) 2022.02.15 [Machine Learning] 모델 평가와 선택(Model Assessment and Selection) (0) 2022.02.14 [Machine Learning] 다중 선형 회귀(Multiple Linear Regression) (0) 2022.02.12 [Machine Learning] 경사 하강법(Gradient Descent) (0) 2022.02.09 [Machine Learning] 최대우도법(Maximum Likelihood Estimation) (0) 2022.02.09