[Machine Learning] 커널 기법(Kernel Method): 커널 트릭(Kernel Trick), 서포트 벡터 머신(Support Vector Machine)

 

기계 학습에서 회귀(Regression)나 $$(\mathbf {x}_1, y_1), \cdots, (\mathbf {x}_N, y_N) \in \mathbb {R}^n \times \mathbb {R}^m$$ 분류(Classification) $$(\mathbf {x}_1, y_1), \cdots, (\mathbf {x}_N, y_N) \in \mathbb {R}^n \times \{ \pm 1 \}$$ 문제에서 사용되는 학습 셋(Training Set)은 모두 미지수의 확률 분포(Probability Distribution) $P(\mathbf {x}, y)$를 따른다. 검정 셋(Test Set)으로 기대 오차(Expected Error)를 다음과 같이 확률 분포에 대해서 계산했을 때, 그 값이 최소화돼야 한다.

$$R [f] = \int \frac {1}{2} |f(\mathbf {x}) - y)|^2 dP(\mathbf {x}, y)$$

이렇게 일반화 오차(Generalization Error)를 최소화하는 방법을 RM(Risk Minimization)이라 하며, 기계 학습에서 핵심적인 개념 중에 하나로 손꼽히고 있다. 

주어진 학습 예제들을 관찰한 후 아직 관찰하지 않은 데이터들까지 잘 예측하는 모델을 설립하는 게 기계 학습의 주 목표인데, 한정된 예제들로부터 좋은 모델을 학습하는 것은 현실적으로 어렵다. 이는 데이터의 실제 확률 분포를 알 수 없기 때문이다. 따라서, 가진 것으로 최적의 모델을 만들기 위해서 RM 대신 ERM(Empirical Risk Minimization)으로 모델을 생성한다. 즉, 데이터의 전체 공간의 오차 대신할 수 있는 학습 데이터로부터 평균 오차를 구한다. 이와 같이 학습 예제로 모델의 오차를 학습 오차(Training Error)라고 한다.

$$R_{emp} [f] = \frac {1}{N} \sum^N_{i = 1} \frac {1}{2} | f(\mathbf {x}_i) - y_i |^2$$

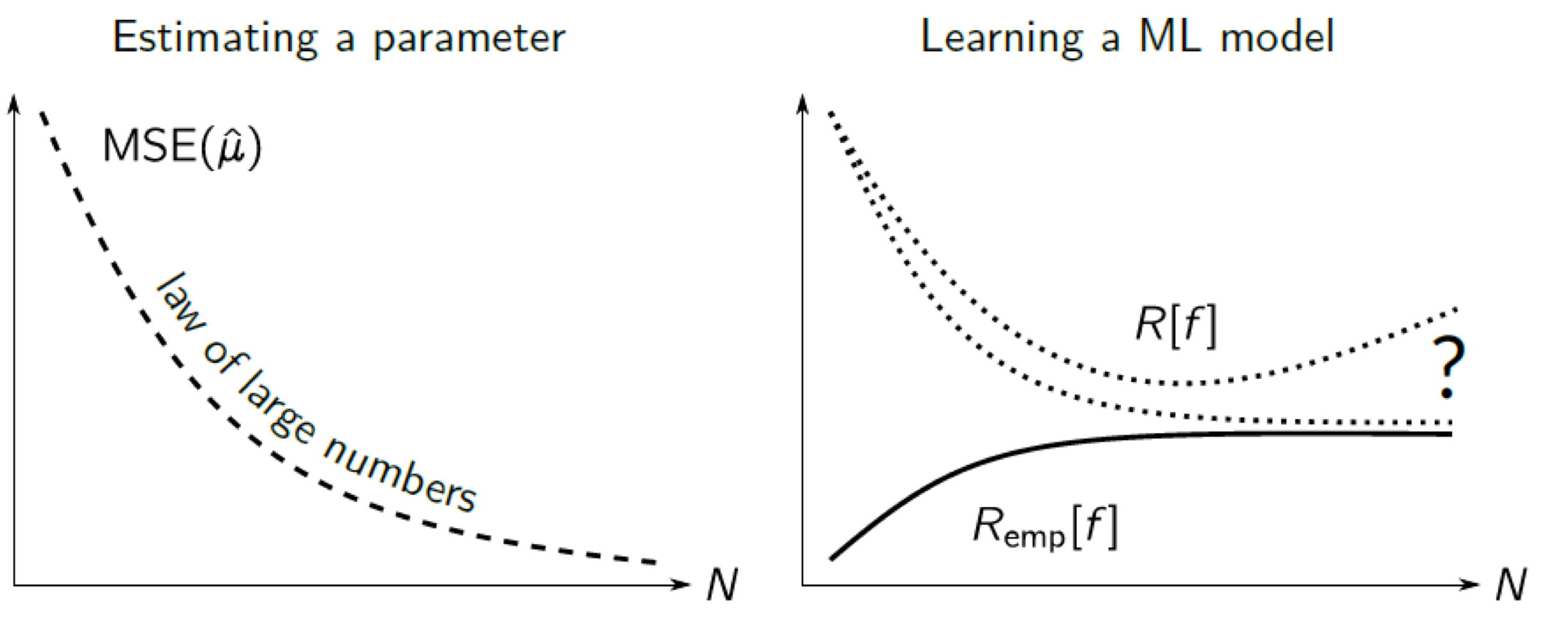
하지만 학습 데이터가 항상 데이터 전체 공간을 잘 대표하는 것은 아니다. 예를 들어, 통계에서 표본의 수가 적을수록 부정확도가 크듯이, 학습 데이터의 수가 적을수록 일반화 오차는 크고 학습 오차는 작다. 결국, 적은 양의 데이터 및 적은 비용으로 좋은 모델을 학습하려면, 오차의 차이가 가장 적은 모델의 학습 데이터 양은 어느 정도이며, 두 오차의 수렴이 얼마나 빠른지, 실제로 수렴은 가능한지 등등에 대해 공부할 필요가 있다.

---

※ [Machine Learning] 모델 평가와 선택(Model Assessment and Selection)

[Machine Learning] 모델 평가와 선택(Model Assessment and Selection)

---

데이터의 양이 무한히 클 때, 학습 오차는 일반화 오차로 수렴한다.

$$R_{emp} [f] \rightarrow R [f] \text { as } N \rightarrow \infty$$

Q. 데이터의 양이 무한히 클 때, ERM의 결과도 RM의 결과와 같은가?
A. 아니오. Vapnik에 의하면 ERM의 결과가 RM의 결과와 같아지려면 균등 수렴(Uniform Convergence)이 추가적으로 요구된다.

---

VC 차원(VC Dimensions)

분류 모델을 위한 VC 이론(Vapnik-Chervonenkis Theory for a Classification Model):
$d$를 $f$의 차원, $N$을 데이터 셋의 개수라 할 때, 최소 $1 - \eta$의 확률로 다음을 만족한다.
$$R [f] \leq R_{emp} [f] + \sqrt {\frac {d(\log \frac {2N}{d} + 1) - \log (\frac {\eta}{4})}{N}}$$
※ $d$를 VC 차원이라고 부른다.

예를 들어, 어떤 함수 $f$의 복잡도가 매우 작을 경우 언더 피팅(Underfitting)으로 인해 학습 오차 $R_{emp}$는 무한대로 커진다. 반대로 $f$의 차원 $d$가 매우 작아지기 때문에 제곱근 항은 0으로 수렴한다. 마찬가지로, 모델의 복잡도가 매우 클 경우에는 오버 피팅(Overfitting)으로 학습 오차 $R_{emp}$는 0으로 수렴하고, 제곱근 항은 폭발적으로 커진다. 두 경우 모두 상한이 무한대로 발산한다.

하지만 모델의 복잡성이 적당히 작고 적당히 크면 일반화 오차의 상한은 어떻게 달라질까? 적당한 값의 $d$를 갖는 $f$를 가정한다면 상한이 상수로 수렴하게 되어 더 정확한 모델을 만들 수 있다.

※ SRM(Structural Risk Minimization)로 모델의 복잡성 줄이기

---

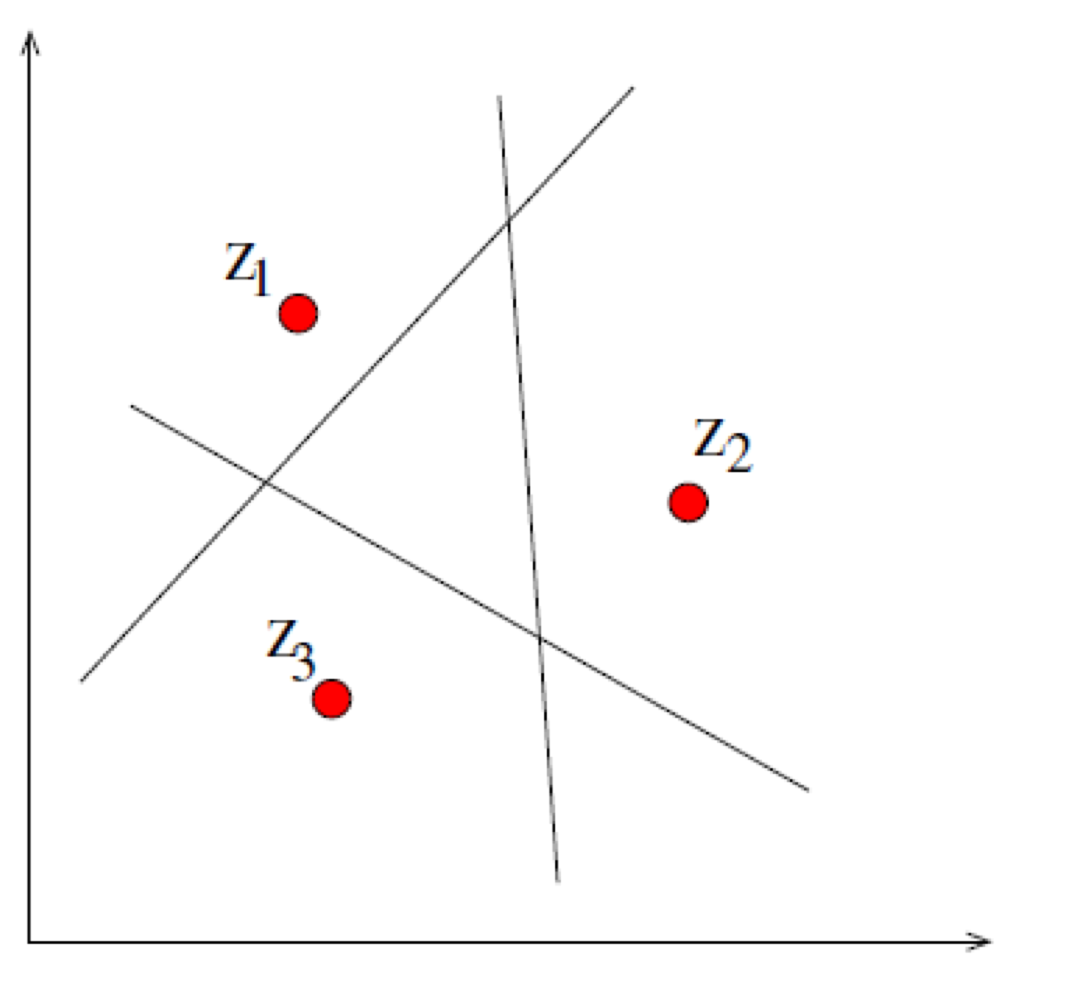
VC 차원 계산의 예시

$\mathbb {R}^2$ 상에서 반공 간(Half-space)을 다음과 같이 표현한다면,

$$f(x, y) = sgn(a + bx + cy), \text { with parameters } a, b, c \in \mathbf {R}$$

공간 상의 임의의 세 비공선점(Non-colinear Points)을 구분할 수 있다. 따라서, VC 차원 $d = 3$이다. 일반화를 하면 $n$ 차원에서 이 모델의 VC 차원 $d$는 $n + 1$이다.

이처럼 VC 차원을 알 수 있다면 일반화 오차의 상한을 공식으로 구할 수 있는데, 복잡한 모델에서의 계산은 생각보다 어렵다. 

---

※ [Machine Learning] 선형 분류(Linear Classification)

[Machine Learning] 선형 분류(Linear Classification)

---

스케일 팩터 제거하기(Removing Scaling Factor)

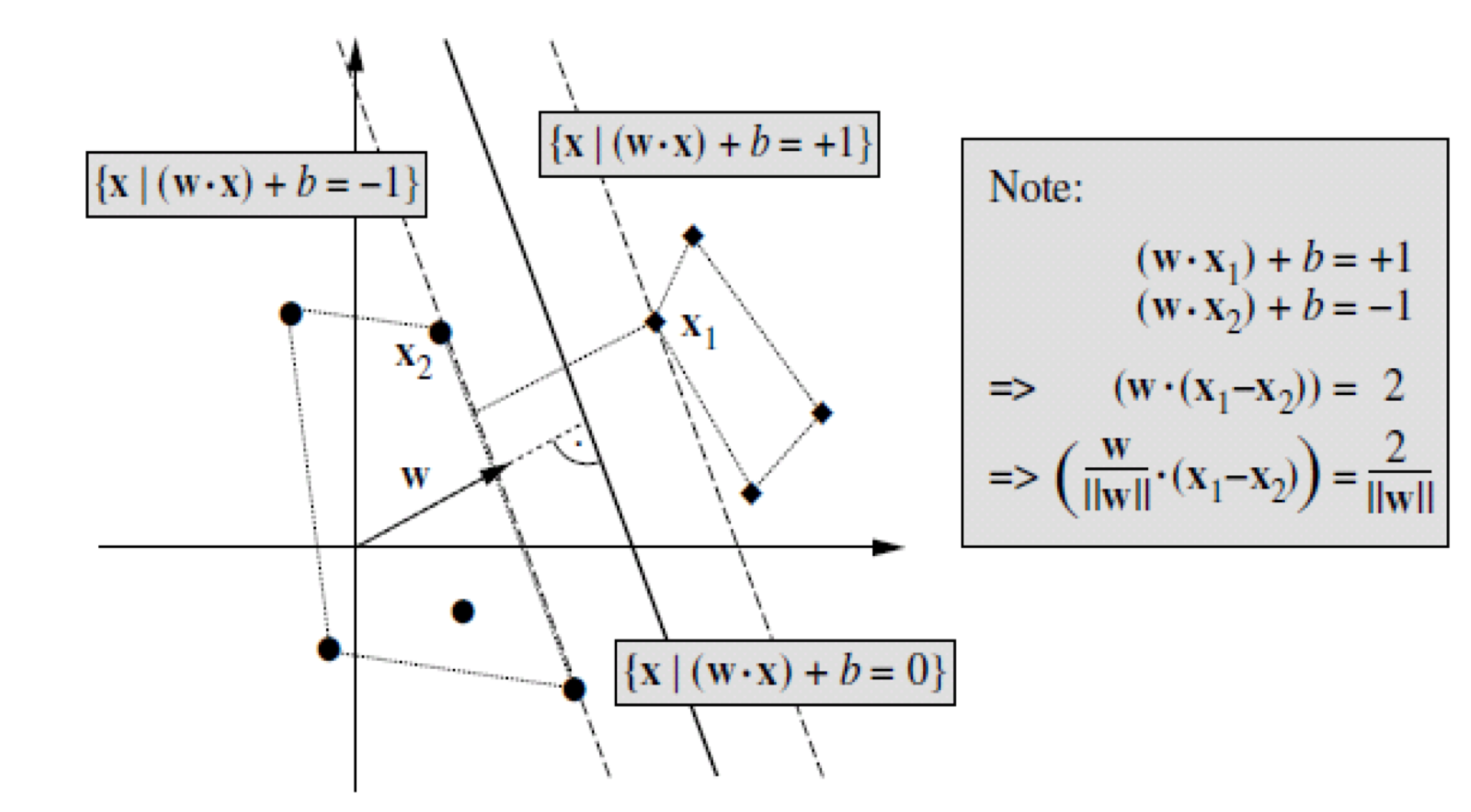
선형 초평면 분류기(Linear Hyperplane Classifier)의 초평면 $y = sgn (\mathbf {wx} + b)$에서 $\mathbf {w}$의 스케일 팩터를 다음과 같이 제거하면 표준 형식(Canonical Form)으로 재정의할 수 있다.

$$\min_{\mathbf {x}_i \in X} |(\mathbf {w x}_i) + b)| = 1$$

즉, 각 클래스에서 초평면에 가장 근접한 점 $\mathbf {x}_1, \mathbf {x}_2$을 꼽아 $\mathbf {w}$의 크기를 제한한다.

---

※ [Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)

[Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)

※ [Machine Learning] 피셔의 선형 판별 분석(Fisher Linear Discriminant Analysis)

[Machine Learning] 피셔의 선형 판별 분석(Fisher Linear Discriminant Analysis)

---

퍼셉트론 인공신경망와 피셔의 선형 판별 분석에서도 배웠듯이, 두 클래스 간 분산(Between Class Scatter)이 클수록 더 좋은 분류기를 만들 수 있었다.

$$\left ( \frac {\mathbf {w}}{||\mathbf {w}||} \cdot (\mathbf {x}_1 - \mathbf {x}_2) \right ) = \frac {2}{||\mathbf {w}||}$$

여기서도 마찬가지로, $\frac {2}{||\mathbf {w}||}$의 값이 클수록 마진(Margin)이 크며, 더욱더 모델의 성능을 향상한다. 결국 노름(Norm) $||\mathbf {w}||$을 최소화해야 한다.

---

LMC(Large Margin Classifier)

초평면 분류기를 위한 VC 이론(Vapnik-Chervonenkis Theory for a Hyperplane Classifier):
$d$를 VC 차원, $n$을 공간 차원, $R$을 데이터를 포함하는 가장 작은 구의 반경이라고 할 때, 표준 형식을 따르는 초평면은 다음과 같은 VC 차원의 조건을 만족한다.
$$d \leq \min \{ [R^2 ||\mathbf {w}||^2 ] + 1, n + 1 \}$$
※ $n + 1$은 $\mathbb {R}^n$ 상에서 반공간을 위한 VC 차원.
※ $R$ 클래스 내의 분산이다.

위와 같이 새로운 조건을 기존 분류 모델을 위한 VC 이론에 대입하면, 마진의 최대화함으로써 최적화된 일반화 모델을 구할 수 있다.

$$\min ||\mathbf {w}||^2$$

$||\mathbf {w}||^2$을 충분히 최소화할 수 있다면, 초평면 분류기를 위한 VC 이론에서 $d$는 $n + 1$가 아닌 $[R^2 ||\mathbf {w} ||^2] + 1$를 따르며, 공간 차원 $n$과 무관하게 최적화된 모델을 만들 수 있다.

---

특성 공간(Feature Space)

이제, 무한한 공간 차원을 가정하여,

$$\begin {align*}
\Phi: \mathbb {R}^N &\rightarrow \mathcal {F} \\
\mathbf {x} &\mapsto \Phi(\mathbf {x})\\
\text {where } N &\ll dim(\mathcal {F}).
\end {align*}$$

회귀 결과 $(\Phi(\mathbf {x}_1), y_1), \cdots, (\Phi(\mathbf {x}_N), y_N) \in \mathcal {F} \times \mathbb {R}^M$ 또는 분류 결과 $\{ \pm 1\}$을 구한다고 하자.

이와 같이 무한한 공간 차원을 갖는 특성 공간 $\mathcal {F}$에 데이터 $\mathbf {x}$를 매핑 후의 데이터 $\Phi(\mathbf {x})$에 대한 모델 $\tilde {f}$을 학습한다.

$$f = \tilde {f} \circ \Phi$$

$\tilde {f}$가 작은 학습 오차와 복잡도가 낮은 학습 모델을 갖도록 $\Phi$를 설정한다면 초고차원임에도 불구하고 매우 간단하게 문제를 해결할 수 있다. 이렇게 공간의 차원이 아니라 모델의 복잡도에 중점을 두어 초고차원의 특성 공간을 활용해 모델의 간단화하는 방법을 서포트 벡터 방식(Support Vector Approach)라고 한다.

비선형 알고리즘의 특성 공간

이차 단항식(Second Order Monomial) 예로 살펴보자. 2차 공간의 데이터를 3차 공간의 특성 공간으로 대응시켰을 때, 다음과 같다.

$$\begin {align*}
\Phi: \mathbb {R}^2 &\rightarrow \mathbb {R}^3 \\
(x_1, x_2) &\mapsto (z_1, z_2, z_3) := (x^2_1, \sqrt {2} x_1 x_2, x^2_2)
\end {align*}$$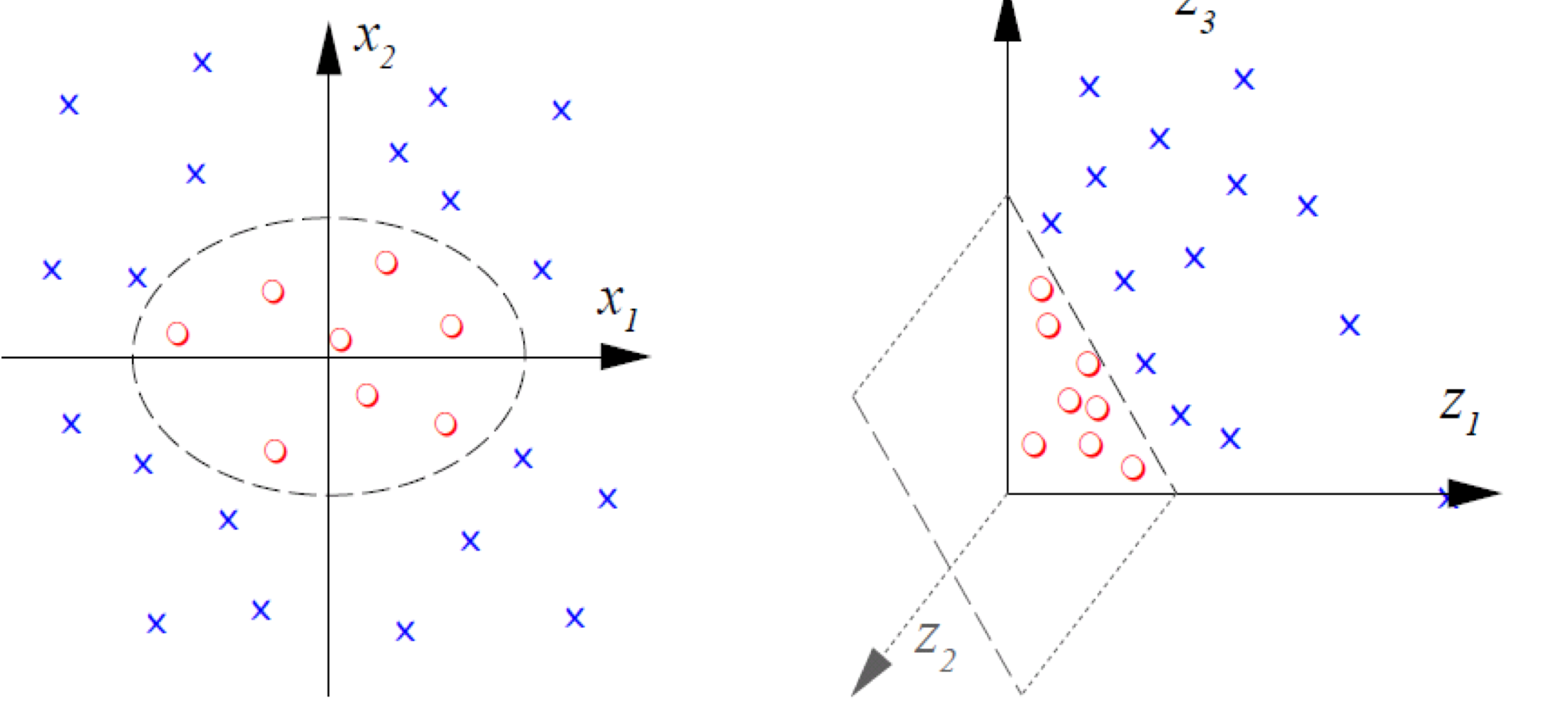

2차 공간에서 타원의 도형을 그렸던 데이터의 분포는 3차 공간에서 선형적으로 표현될 수 있다.

---

커널 트릭(Kernel Trick)

$$\begin {align*}
(\Phi (\mathbf {x}) \cdot \Phi (\mathbf {y})) &= (x^2_1, \sqrt {2} x_1 x_2, x^2_2)(y^2_1, \sqrt {x} y_1 y_2, y^2_2)^{\top} \\
&= (\mathbf {x} \cdot \mathbf {y})^2 \\
&= :k(\mathbf {x}, \mathbf {y})
\end {align*}$$

특성 공간의 스칼라 곱(Scalar Product)은 $\mathbb {R}^2$상에서 계산할 수 있다.

※ 커널 트릭은 머서 커널(Mercer Kernel) $k(\mathbf {x}, \mathbf {y})$으로만 가능하다.

---

머서 커널(Mercer Kernel)

$L_2(\mathcal {D})$상의 양의 적분 연산자(Positive Integral Operator)의 연속적인 커널(Continuous Kernel)을 $k$라고 할 때,

$$\int f(\mathbf {x}) k(\mathbf {x}, \mathbf {y}) f(\mathbf {y}) d\mathbf {x} d\mathbf {y} \geq 0, \text { for } f \neq 0$$

$k$를 다음과 같이 쓸 수 있다.

$$k (\mathbf {x}, \mathbf {y}) = \sum^{N_{\mathcal {F}}}_{i = 1} \lambda_i \phi_i(\mathbf {x}) \phi_i (\mathbf {y})$$

※ $\lambda_i > 0$이고 $N_{\mathcal {F}} \in \mathbb {N}$이거나 $N_{\mathcal {F}} = \infty$다.

이때,

$$\Phi(\mathbf {x}) := \begin {pmatrix} \sqrt {\lambda_1} \phi_1(\mathbf {x}) \\ \sqrt {\lambda_2} \phi_2(\mathbf {x}) \\ \vdots \end {pmatrix}$$

는 $(\Phi (\mathbf {x}) \cdot \Phi (\mathbf {y})) = k(\mathbf {x}, \mathbf {y})$을 만족한다.

머서 커널의 모든 고유값(Eigenvalue)의 값은 양수이어야 한다. 만약 하나

---

커널의 예시

커널은 정규화 연산자(Regularization Operator)에 해당하며, 푸리에 공간(Fourier Space) 내에서 표현된다. 

다항식 커널(Polynomial Kernel)

$$k(\mathbf {x}, \mathbf {y}) = (\mathbf {x} \cdot \mathbf {y} + c)^d$$

※ 유한 공간 차원

RBF 커널(Radial Basis Function Kernel)

$$k(\mathbf {x}, \mathbf {y}) = \exp (- \frac {||\mathbf {x} - \mathbf {y}||^2}{2 \sigma^2} )$$

※ 무한 공간 차원

역 다중이차 커널(Inverse Multiquadric Kernel)

$$k (\mathbf {x}, \mathbf {y}) = \frac {1}{\sqrt {||\mathbf {x} - \mathbf {y}||^2 + c^2}}$$

---

커널 트릭의 또 다른 예시

데이터 셋 $\mathcal {D} = \{ \mathbf {x}_1, \cdots, \mathbf {x}_N \}$이 있을 때, 특성 공간 상에서 평균까지의 제곱 거리를 계산하려고 한다. 

$$f(\mathbf {x}) = || \Phi(\mathbf {x}) - \frac {1}{N} \sum^N_{i = 1} \Phi(\mathbf {x}_i)||^2$$

$f(\mathbf {x})$에 대한 식은 다음과 같이 커널에 대해서 재정리할 수 있다.

$$f(\mathbf {x}) = \underbrace{<\Phi(\mathbf {x}), \Phi(\mathbf {x})>}_{k (\mathbf {x}, \mathbf {x})} - \frac {2}{N} \sum^N_{i = 1} \underbrace {<\Phi(\mathbf {x}), \Phi(\mathbf {x}_i)>}_{k (\mathbf {x}, \mathbf {x}_i)} + \frac {1}{N^2} \sum^N_{i = 1} \sum^N_{j = 1} \underbrace {<\Phi(\mathbf {x}_i), \Phi (\mathbf {x}_j)>}_{k(\mathbf {x}_i, \mathbf {x}_j)}$$

※ $|| \mathbf {a} - \mathbf {b} ||^2 = <\mathbf {a}, \mathbf {a}> - 2 <\mathbf {a}, \mathbf {b}> + <\mathbf {b}, \mathbf {b}>$

---

$\mathcal {F}$ 상의 초평면 $y = sgn (\mathbf {w} \cdot \Phi(\mathbf {x}) + b)$

LMC에 커널 트릭을 적용하면 노름은 최소화되어야 하고, $$\min ||\mathbf {w} ||^2,$$ 올바르게 분류를 하려면 다음 조건을 만족해야 한다. $$y_i \cdot [(\mathbf {w} \cdot \Phi(\mathbf {x}_i)) + b] \geq 1 \text { for } i = 1 \cdots N.$$

모든 조건을 고려해 라그랑주 승수법(Lagrange Multiplier)으로 최대 마진을 보장하면서 올바르게 분류까지 하는 식을 하나로 표현하였다.

$$L(\mathbf {w}, b, \mathbf {\alpha}) = \frac {1}{2} ||\mathbf {w}||^2 - \sum^N_{i = 1} \alpha_i (y_i \cdot ((\mathbf {w} \cdot \Phi(\mathbf {x}_i)) + b) - 1)$$

※ $||\mathbf {w}||^2$ 앞에 $\frac {1}{2}$는 계산의 용이성을 위해 추가되었다.

라그랑주 승수법을 풀기 위해 각 모수(Parameter)에 대해 편미분 = 0을 적용하면 다음과 같다.

$$\begin {align*}
\frac {\partial}{\partial b} L (\mathbf {w}, b, \mathbf {\alpha}) = 0,&\ \ \frac {\partial}{\partial \mathbf {w}} L (\mathbf {w}, b, \mathbf {\alpha}) = 0 \\
i.e.\ \sum^N_{i = 1} \alpha_i y_i = 0 &\ \ \text {and  } \mathbf {w} = \sum^N_{i = 1} \alpha_i y_i \Phi(\mathbf {x}_i)
\end {align*}$$

※ 무한의 특성 공간에 대응시킨 데이터의 분류 문제는 유한의 공간에서의 계산 ($\sum^N_{i = 1}$)을 통해서 도출이 가능하다.

두 개의 새로운 식을 원래 식 $L$에 대입하여 라그랑주의 쌍대 문제(Dual Problem)을 계산한다.

---

SVM(Support Vector Machine): 슬랙 변수(Slack Variable)를 사용한 $\mathcal {F}$ 상의 초평면 $y = sgn (\mathbf {w} \cdot \Phi(\mathbf {x}) + b)$

인공 신경망(Artificial Neural Network)에서 사용되는 힌지 손실(Hinge Loss)에서 공부했듯이, 직선의 결정 경계(Decision Boundary)로 분류가 되지 않는 문제에 개별적으로 오차의 여유를 부여해서 분류기의 효율성을 높일 수 있다. 이때, 관대한 결정 경계를 조정할 수 있는 변수를 슬랙 변수(Slack Variable)라고 한다. 

LMC에 커널 트릭과 슬랙 변수를 적용하면, 노름과 슬랙 변수는 최소화되어야 하고, $$\min ||\mathbf {w} ||^2 + C \sum^N_{i = 1} {\xi_i}^p,$$ 올바르게 분류를 하려면 다음 조건을 만족해야 한다. $$y_i \cdot [(\mathbf {w} \cdot \Phi(\mathbf {x}_i)) + b] \geq 1 - \xi_i \text { and } \xi_i \geq 0 \text { for } i = 1 \cdots N.$$

모든 조건을 고려해 라그랑주 승수법으로 최대 마진을 보장하면서 올바르게 분류까지 하는 식을 하나로 표현하였다.

$$L(\mathbf {w}, b, \mathbf {\alpha}) = \frac {1}{2} ||\mathbf {w}||^2 - \sum^N_{i = 1} \alpha_i (y_i \cdot ((\mathbf {w} \cdot \Phi(\mathbf {x}_i)) + b) - 1)$$

※ $||\mathbf {w}||^2$ 앞에 $\frac {1}{2}$는 계산의 용이성을 위해 추가되었다.

라그랑주 승수법을 풀기 위해 각 모수에 대해 편미분 = 0을 적용하면 다음과 같다.

$$\begin {align*}
\frac {\partial}{\partial b} L (\mathbf {w}, b, \mathbf {\alpha}) = 0,&\ \ \frac {\partial}{\partial \mathbf {w}} L (\mathbf {w}, b, \mathbf {\alpha}) = 0 \\
i.e.\ \sum^N_{i = 1} \alpha_i y_i = 0 &\ \ \text {and  } \mathbf {w} = \sum^N_{i = 1} \alpha_i y_i \Phi(\mathbf {x}_i)
\end {align*}$$

※ 무한의 특성 공간에 대응시킨 데이터의 분류 문제는 유한의 공간에서의 계산 ($\sum^N_{i = 1}$)을 통해서 도출이 가능하다.

두 개의 새로운 식을 원래 식 $L$에 대입하여 라그랑주의 쌍대 문제을 계산한다.

---

SVM의 쌍대 문제(Dual Problem)

※ [Machine Learning] SVM(Support Vector Machine): 원초 문제에서 쌍대 문제로(From the Primal to the Dual Problem)

[Machine Learning] SVM(Support Vector Machine): 원초 문제에서 쌍대 문제로(From the Primal to the Dual Problem)

---

$$\begin {align*}
\max W(\alpha) = \max \sum^N_{i = 1} \alpha_i - \frac {1}{2} \sum^N_{i, j = 1} \alpha_i \alpha_j y_i y_j k (\mathbf {x}_i, \mathbf {x}_j), \\ \text {s.t.} \ C \geq \alpha_i \geq 0,\ i = 1 \cdots N, \text { and } \sum^N_{i = 1} \alpha_i y_i = 0.
\end {align*}$$

$$\begin {align*}
y_i \cdot [(\mathbf {w} \cdot \Phi (\mathbf {x}_i)) + b] &> 1 & \Rightarrow \alpha_i = 0 & \rightarrow \mathbf {x}_i \text{ irrelevant} \\
y_i \cdot [(\mathbf {w} \cdot \Phi (\mathbf {x}_i)) + b] &= 1 & \text{(on / in margin)} & \rightarrow \mathbf {x}_i \text { SV}
\end {align*}$$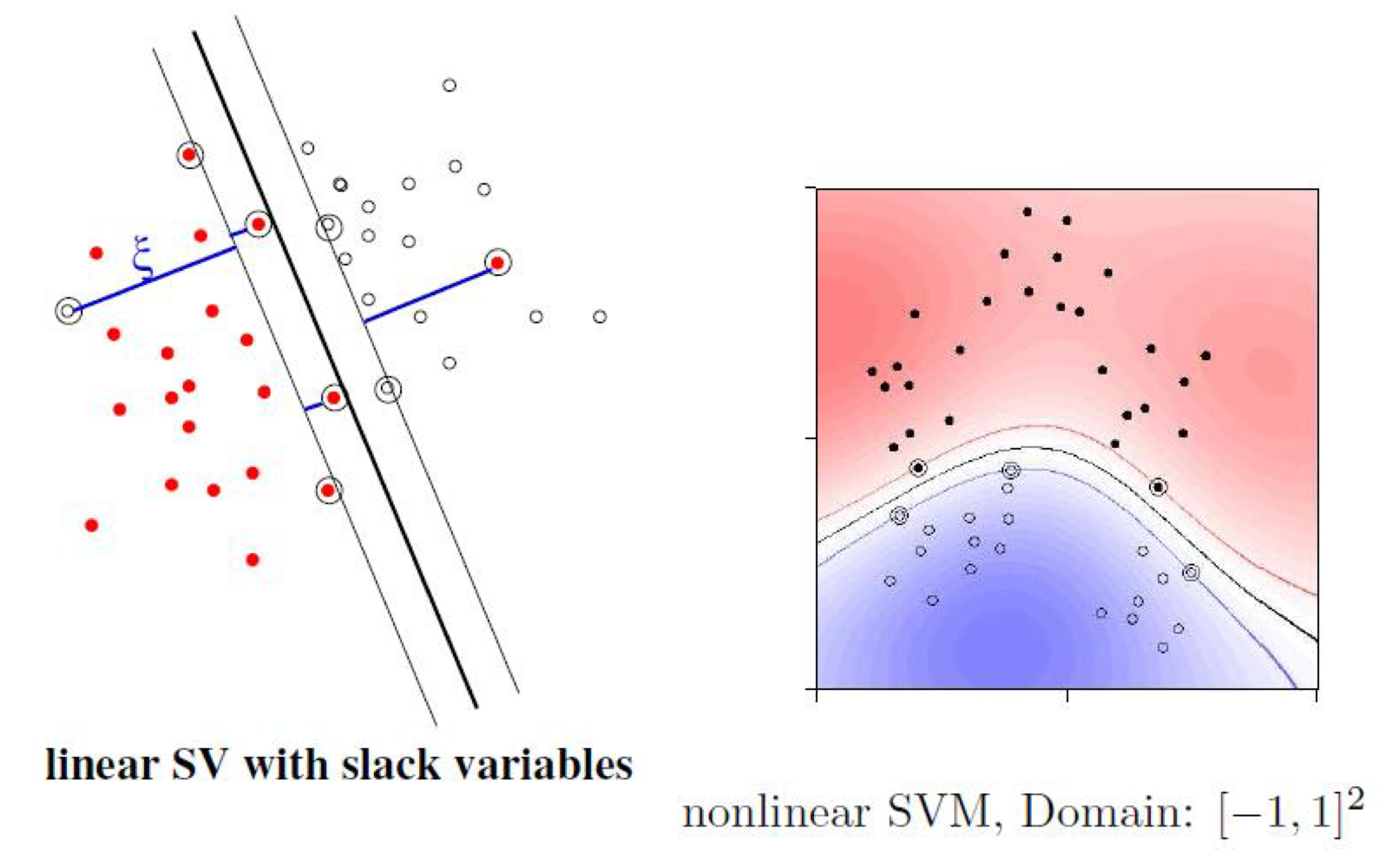

RBF 커널의 SVM 예제

---

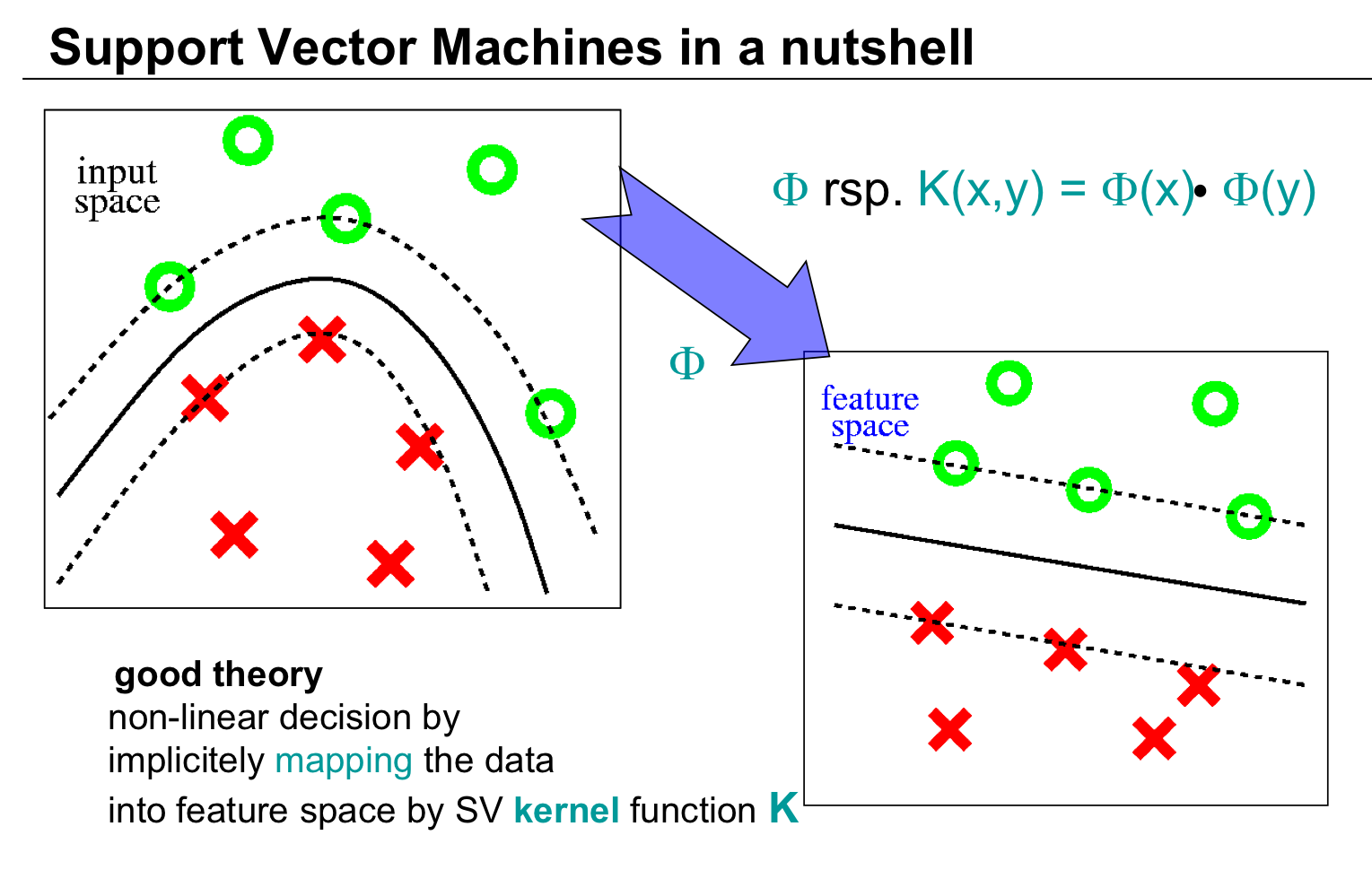
SVM과 커널 트릭(SVM and the Kernel Trick)

• 안장점(Saddle Point): $\mathbf {w} = \sum^N_{i = 1} \alpha_i y_i \Phi(\mathbf {x}_i)$
• $\mathcal {F}$ 상의 초평면: $y = sgn(\mathbf {w} \cdot \Phi(\mathbf {x}) + b)$
• 커널 트릭
  $$\begin {align*}
  f (\mathbf {x}) &= sgn(\mathbf {w} \cdot \Phi(\mathbf {x}) + b) \\
  &= sgn \left ( \sum^N_{i = 1} \alpha_i y_i \Phi(\mathbf {x}_i) \cdot \Phi (\mathbf {x}) + b \right ) \\
  &= sgn \left ( \sum_{i \in \text{#SVs}} \alpha_i y_i k(\mathbf {x}, \mathbf {x}_i) + b \right )
  \end {align*}$$
• N이 아니라 몇개의 SV에 대해서만 계산하면 된다. 

---

SVM의 구현 문제

행렬 $\mathbf {\alpha} = (\alpha_1, \cdots, \alpha_N)^{\top}$, 행렬 $\mathbf {y} = (y_1, \cdots, y_N)^{\top}$, $H_{ij} = y_i y_j k(\mathbf {x}_i, \mathbf {x}_j)$를 원소를 갖는 행렬 $\mathbf {H}$, 1로만 $N$ 크기만큼 구성된 벡터 $\mathbf {1}$를 가정할 때, SVM 문제는 다음과 같아진다.

$$\begin {align*}
\max_{\mathbf {\alpha}} &\mathbf {1}^{\top} \mathbf {\alpha} - \frac {1}{2} \mathbf {\alpha}^{\top} \mathbf {H \alpha}, \label {e1} \tag {1} \\
\text {subject to } &\mathbf {y}^{\top} \mathbf {\alpha} = 0, \label {e2} \tag {2} \\
&\mathbf {\alpha} - C \mathbf {1} \leq 0, \label {e3} \tag {3} \\
&\mathbf {\alpha} \geq 0. \label {e4} \tag {4}
\end {align*}$$

$M$ 값이 클 때, 해당 문제를 학습하는 하는데 매우 오래 걸린다. 학습 속도를 가속화하기 위해서 데이터를 배치(Batch)로 나누어 계산할 수 있다. 

각 반복마다 현재 학습하고 있는 변수 $\mathbf {\alpha}_B$와 나머지 변수 $\mathbf {\alpha}_N$를 가정할 때, 다음과 같이 $\mathbf {H}$를 분할할 수 있다.

$$\mathbf {H} = \begin {bmatrix} \mathbf {H}_{BB} & \mathbf {H}_{BN} \\ \mathbf {H}_{NB} & \mathbf {H}_{NN} \end {bmatrix}$$

SVM 문제는 다음과 같이 쓴다.

$$\begin {align*}
\max_{\mathbf {\alpha}} &(\mathbf {1}^{\top}_B - \mathbf {\alpha}^{\top}_N \mathbf {H}_{NB}) \mathbf {\alpha}_B - \frac {1}{2} \mathbf {\alpha}^{\top}_B \mathbf {H}_{BB} \mathbf {\alpha}_B, \label {e5} \tag {5} \\
\text {subject to } &\mathbf {y}^{\top}_B \mathbf {\alpha}_B = - \mathbf {y}_N \mathbf {\alpha}_N, \label {e6} \tag {6} \\
&\mathbf {\alpha}_B - C \mathbf {1}_B \leq 0, \label {e7} \tag {7} \\
&\mathbf {\alpha}_B \geq 0. \label {e8} \tag {8}
\end {align*}$$

현재 학습하고 있는 셋을 제외하고 나머지 $\mathbf {H}_{BN}, \mathbf {H}_{NN}$는 고정한 채 반복해서 최적화한다.

---

존 플랫의 SMO(John Platt's Sequential Minimal Optimization)

현재 학습하고 있는 셋에서 두 점만을 사용해서 분석적으로 최적화 문제를 계산한다.

우선 $y_1 \neq y_2$인지 $y_1 = y_2$인지 경우를 나누고, 식 $\ref {e6}$의 조건에 의해 점들이 $\alpha_1 - \alpha_2 = \gamma$ 상에 있거나 $\alpha_1 + \alpha_2 = \gamma$ 상이 있다.

Q. 어떤 기준으로 두 점을 선출하는가?
A. 최대한 두 분류의 결과가 일치하지 않도록 하는 두 점을 선택한다.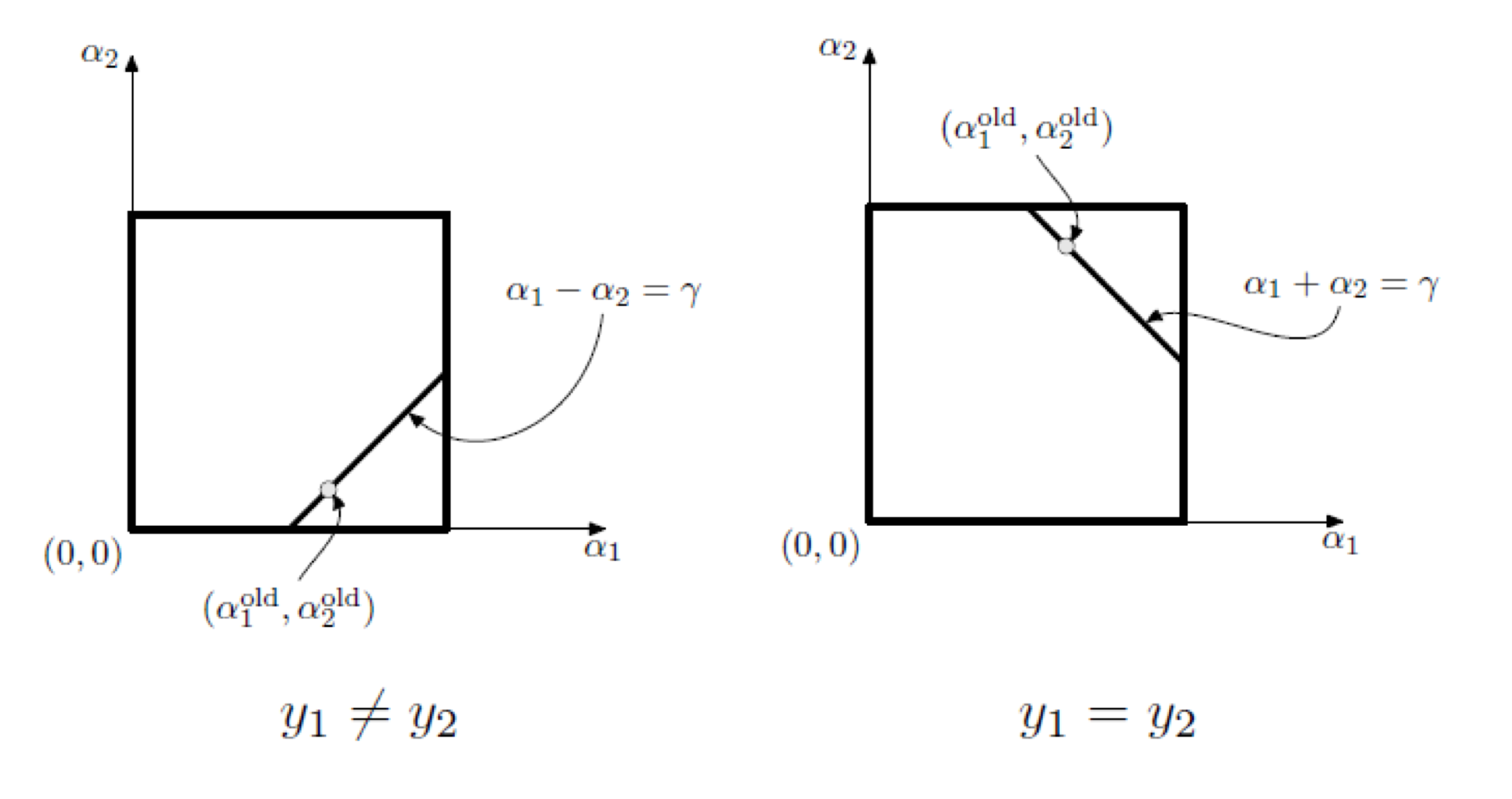

$\alpha_2$에 대해서 정리하면 다음과 같다.

$$\alpha^{new}_2 = \alpha^{old}_2 - \frac {y_2 (E_1 - E_2)}{\eta}$$

where

$$\begin {align*}
E_1 &= \sum^N_{j = 1} y_j \alpha_j k(\mathbf {x}_1, \mathbf {x}_j) + b - y_1 \\
E_2 &= \sum^N_{j = 1} y_j \alpha_j k(\mathbf {x}_2, \mathbf {x}_j) + b - y_2 \\
\eta &= 2 k (\mathbf {x}_1, \mathbf {x}_2) - k (\mathbf {x}_1, \mathbf {x}_1) - k (\mathbf {x}_2, \mathbf {x}_2)
\end {align*}$$

그 후에 유계 제약 조건을 처리해야 한다. 기하학에 따라 다음과 같이 $\alpha_2$의 값의 하한과 상한을 계산한다.

$$\begin {align*}
L &= \begin {cases}
\max (0, \alpha^{old}_2 - \alpha^{old}_1), & \text {if } y_1 \neq y_2, \\
\max (0, \alpha^{old}_2 + \alpha^{old}_1 - C), & \text {if } y_1 = y_2, \\
\end {cases} \\
H &= \begin {cases}
\min (C, C + \alpha^{old}_2 - \alpha^{old}_1), & \text {if } y_1 \neq y_2, \\
\min (C, \alpha^{old}_2 + \alpha^{old}_1), & \text {if } y_1 = y_2.
\end {cases}
\end {align*}$$

제약된 최적은 제약이 없는 최적을 선분의 끝에서 찾는다.

$$\alpha^{new}_2 := \begin {cases}
H, & \text {if} \alpha^{new}_2 \geq H, \\
L, & \text {if} \alpha^{new}_2 \leq L, \\
\alpha^{new}_2, & \text {otherwise}.
\end {cases}$$

마지막으로 $\alpha^{new}_1$의 값을 계산한다.

$$\alpha^{new}_1 = \alpha^{old}_1 + y_1 y_2 (\alpha^{old}_2 -\alpha^{new}_2)$$

---

단일 클래스 SVM(One-class SVM)

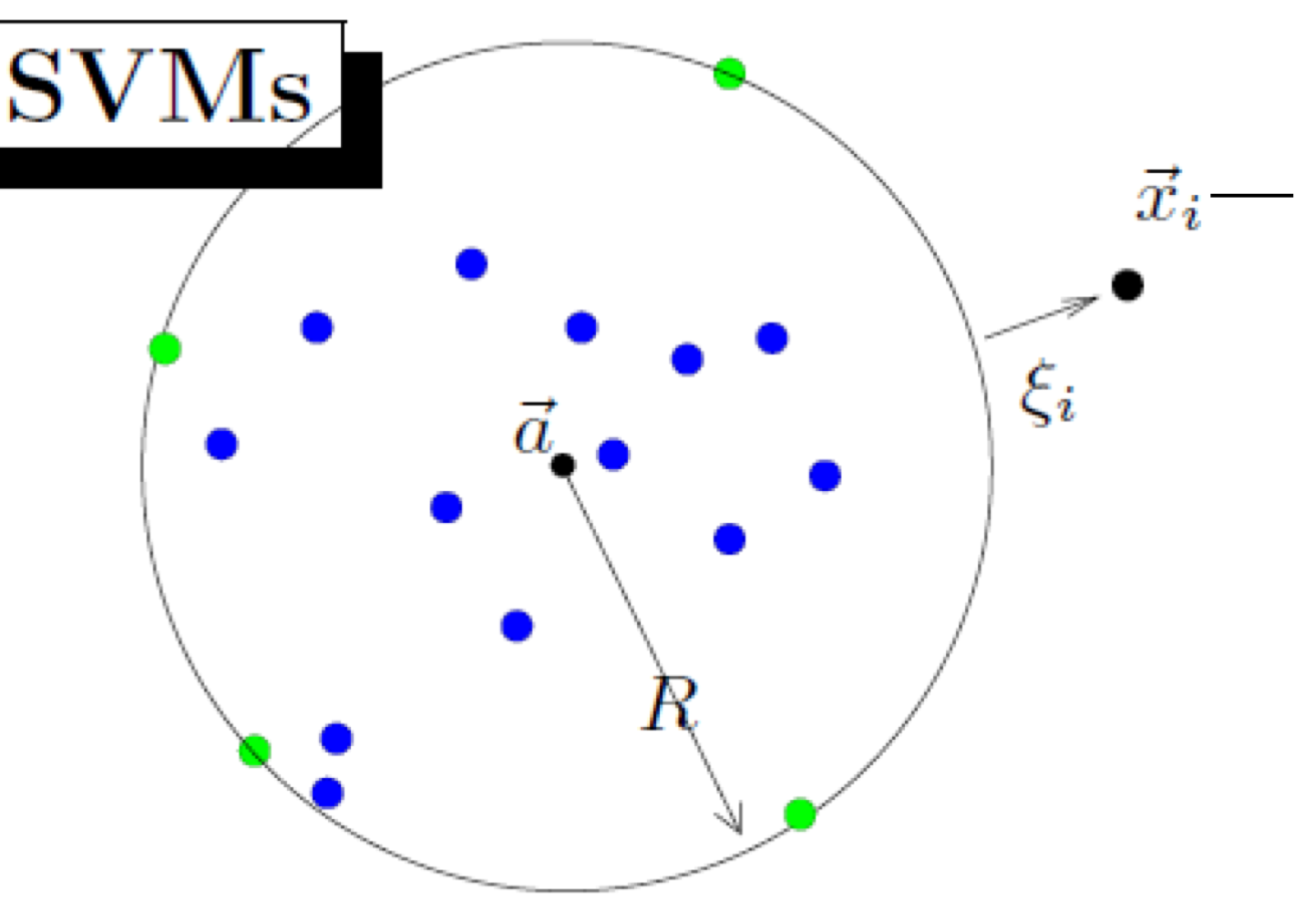
단일 클래스 SVM에서는 데이터가 정상적인지 비정상적인지 분석한다.

데이터를 초구(Hypersphere) 안에 맞추려고 한다.

$$\begin {align*}
\max_{\alpha} &\sum^N_{i = 1} \alpha_i k(\mathbf {x}_i, \mathbf {x}_i) - \frac {1}{2} \sum^M_{i, j = 1} \alpha_i \alpha_j k (\mathbf {x}_i, \mathbf {x}_j), \\
\text {subject to } &0 \leq \alpha_i \leq C, i = 1, \cdots, N, \\
&\sum^{N}_{i = 1} \alpha_i = 1.
\end {align*}$$

새로운 데이터가 어느 클래스에 속할 것인지는 다음 식으로 판단한다.

$$f(\mathbf {x}) = sign (R^2 - k(\mathbf {x}, \mathbf {x})  + 2 \sum_i \alpha_i k(\mathbf {x}, \mathbf {x}_i) - \sum_{i, j} \alpha_i \alpha_j k (\mathbf {x}_i, \mathbf {x}_j))$$

---

커널 PCA(Kernel Principle Component Analysis)

※ [Machine Learning] PCA(Principal Component Analysis)

[Machine Learning] PCA(Principal Component Analysis)

---

데이터 $\mathbf {x}_1, \cdots, \mathbf {x}_N$, 매핑 함수(Mapping Function) $\Phi: \mathbb {R}^D \rightarrow \mathcal {F}$, 공분산 행렬(Covariance Matrix) $C = \frac {1}{N} \sum^N_{j = 1} \Phi(\mathbf {x}_j) \Phi (\mathbf {x}_j)^{\top}$를 가정할 때,

고유값 찾기 문제는 다음과 같다. (※ $\mathbf {V}$는 특성 공간 상의 고유벡터(Eigenvector))

$$\lambda \mathbf {V} = C \mathbf {V} = \frac {1}{N} \sum^N_{j = 1} (\Phi(\mathbf {x}_j) \cdot \mathbf {V}) \Phi(\mathbf {x}_j)$$

$\lambda \neq 0$일 때, $\mathbf {V} \in span \{ \Phi(\mathbf {x}_1), \cdots, \Phi(\mathbf {x}_N)\}$이다. 따라서, $\mathbf {V} = \sum^N_{i = 1} \alpha_i \Phi(\mathbf {x}_i)$이다.

양변의 왼쪽에 $N$과 $\Phi(\mathbf {x}_k)$을 곱하면 다음과 같다.

$$N \lambda (\Phi(\mathbf {x}_k) \cdot \mathbf {V}) = N (\Phi (\mathbf {x}_k) \cdot C \mathbf {V}) \ \text { for all } k = 1, \cdots, N$$

$$\begin {align*}
\therefore N \lambda (\sum^N_{i = 1} \Phi(\mathbf {x}_k) \cdot \Phi(\mathbf {x}_i)) \mathbf {\alpha} = (\Phi (\mathbf {x}_k) \cdot \sum^N_{j = 1} \sum^N_{i = 1} (\Phi(\mathbf {x}_j) \cdot  \Phi(\mathbf {x}_i))\Phi(\mathbf {x}_j)) \mathbf {\alpha} \label {this} \tag {*} \\
\text { for all } k = 1, \cdots, N
\end {align*}$$

이제 커널 트릭을 적용하기 위해서 새로운 $N \times N$ 행렬을 정의한다.

$$K_{ij} := (\Phi (\mathbf {x}_i) \cdot \Phi (\mathbf {x}_j)) = k (\mathbf {x}_i, \mathbf {x}_j)$$

식 $\ref {this}$을 $N \lambda K \mathbf {\alpha} = K^2 \mathbf {\alpha}$로 쓸 수 있다. (※ $\mathbf {\alpha} = (\alpha_1, \cdots, \alpha_N)^{\top}$)

양변을 K로 나누면 결국 $N \lambda \mathbf {\alpha} = K \mathbf {\alpha}$의 문제를 푸는 것이다. 이때, $K$를 선형 커널은 사용하면 $N \times N$ 행렬의 고유값을 찾는 것과 같다. 초고차원이지만 데이터의 양이 작은 경우 선형 커널을 이용해 PCA하면 효과가 크다.

직교성(Orthonormal)을 보장하기 위해 벡터들을 정규화한다.

$$(\mathbf {V}^k \cdot \mathbf {V}^k) = 1 \Leftrightarrow N \lambda_k (\mathbf {\alpha}^k \cdot \mathbf {\alpha}^k) = 1$$ 

고유벡터에 정사영을 계산한다.

$$\mathbf {V}^k = \sum^M_{i = 1} \alpha^k_i \Phi(\mathbf {x}_i)$$

새로운 데이터 $\mathbf {x}$마다 커널 PCA 구성요소(Kernel PCA Componenets)를 다음과 같이 얻는다.

$$\begin {align*}
f_k (\mathbf {x}) = (\mathbf {V}^k \cdot \Phi(\mathbf {x})) &= \sum^N_{i = 1} \alpha^k_i (\Phi(\mathbf {x}_i) \cdot \Phi (\mathbf {x})) \\
&= \sum^N_{i = 1} \alpha^k_i k (\mathbf {x}_i, \mathbf {x})
\end {align*}$$

Q. 특성 공간에서 어떻게 데이터들을 정렬할까?
A. $$\tilde {\Phi} (\mathbf {x}_i) := \Phi (\mathbf {x}_i) - \underbrace {\frac {1}{N} \sum^N_{i = 1} \Phi(\mathbf {x}_i)}_{\begin {align*} \text{Not kernerlizable} \\ \therefore \text {Redefine } \Phi \end {align*}}$$
$K$를 $(1_N)_{ij} := \frac {1}{N}$을 이용해서 새로운 커널 $\tilde {K}$을 정의한다.
$$\tilde {K}_{ij} = K - 1_N K - K 1_N + 1_N K 1_N$$
특성 공간에서 정렬된 데이터들로 PCA의 고유값 문제를 푼다.

---

1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.

2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.